Замечательные эквивалентности в пределах

Для решения практических примеров потребуется таблица замечательных эквивалентностей. Не многочленом единым жив студент, поэтому поле дальнейшей деятельности будет очень широким. Сначала с помощью теории бесконечно малых эквивалентных функций перещёлкаем примеры первой части урока Замечательные пределы. Примеры решений, в которой были найдены следующие пределы:

1) Решим предел . Заменим бесконечно малую функцию числителя на эквивалентную бесконечно малую функцию :

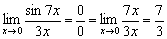
Почему можно провести такую замену? Потому что бесконечно близко вблизи нуля график функции практически совпадает с графиком функции .

В этом примере мы использовали табличную эквивалентность 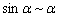, где . Удобно, что в качестве параметра «альфа» может выступать не только «икс», но и сложная функция, которая стремится к нулю.

2) Найдём предел . В знаменателе используем эту же эквивалентность 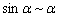, в данном случае :

Обратите внимание, что синус изначально находился под квадратом, поэтому на первом шаге тоже необходимо целиком поместить под квадрат.

Не забываем и про теорию: в первых двух примерах получены конечные числа, значит, числители и знаменатели одного порядка малости.

3) Найдём предел 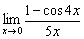. Заменим бесконечно малую функцию числителя эквивалентной функцией , где :

Здесь числитель более высокого порядка малости, чем знаменатель. Лилипут (и эквивалентный ему лилипут ) достигает нуля быстрее, чем .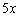

4) Найдём предел . Заменим бесконечно малую функцию числителя эквивалентной функцией , где :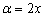

А здесь, наоборот, знаменатель более высокого порядка малости, чем числитель, карлик убегает к нулю быстрее карлика (и эквивалентного ему карлика ).

Следует ли использовать замечательные эквивалентности на практике? Следует, но далеко не всегда. Так, решение не очень сложных пределов (наподобие только что рассмотренных) нежелательно решать через замечательные эквивалентности. Вас могут упрекнуть в халтуре и заставить прорешать их стандартным образом с помощью тригонометрических формул и первого замечательного предела. Однако с помощью рассматриваемого инструмента очень выгодно осуществлять проверку решения или даже сразу узнавать правильный ответ. Характерен Пример №14 урока Методы решения пределов:

На чистовике целесообразно оформить немаленькое полное решение с заменой переменной. Но готовый ответ лежит на поверхности – мысленно используем эквивалентность : .

И ещё раз геометрический смысл: почему в числителе функцию допустимо заменить функцией ? Бесконечно близко вблизи нуля их графики можно отличить разве что под мощным микроскопом.

Помимо проверки решения, замечательные эквивалентности используются ещё в двух случаях:

– когда пример достаточно сложен или вообще неразрешим обычным способом;
– когда замечательные эквивалентности требуется применить по условию.

Рассмотрим более содержательные задания:

Пример 4

Найти предел

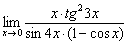
На повестке дня неопределённость «ноль на ноль» и ситуация погранична: решение можно провести стандартно, но преобразований будет много. С моей точки зрения, здесь вполне уместно использовать замечательные эквивалентности:

Заменим бесконечно малые функции эквивалентными функциями. При :

Вот и всё!

Единственный технический нюанс: изначально тангенс находился в квадрате, поэтому после замены аргумент 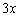тоже необходимо возвести в квадрат.

Пример 5

Найти предел

Данный предел разрешим через тригонометрические формулы и замечательные пределы, но решение опять же будет не сильно приятным. Это пример для самостоятельного решения, будьте особенно внимательными в ходе преобразования числителя. Если возникнет путаница со степенями, представьте его в виде произведения:

Пример 6

Найти предел

А вот это уже тяжёлый случай, когда провести решение стандартным образом весьма непросто. Используем замечательные эквивалентности:

Заменим бесконечно малые эквивалентными. При :

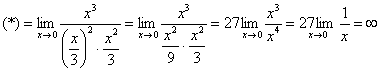
Получена бесконечность, значит, знаменатель более высокого порядка малости, чем числитель.

Резво практика пошла без верхней одежды =)

Пример 7

Найти предел

Это пример для самостоятельного решения. Подумайте, как разобраться с логарифмом;-)

Не редкость, когда замечательные эквивалентности используются в комбинации с другими методами решения пределов:

Пример 8

Найти предел функции, используя эквивалентные бесконечно малые величины и другие преобразования

Заметьте, что здесь требуется применить замечательные эквивалентности по условию.

Решаем:

На первом шаге используем замечательные эквивалентности. При :

С синусом всё понятно: . Что делать с логарифмом? Представим логарифм в виде 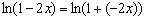и применим эквивалентность . Как вы понимаете, в данном случае и

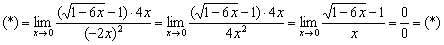
На втором шаге применим приём, рассмотренный ещё на уроке Пределы функций. Примеры решений. Умножим числитель и знаменатель на сопряженное выражение:

Готово.

Пример 9

Найти предел функции, используя эквивалентные бесконечно малые величины и другие преобразования

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Иногда замечательные эквивалентности приходится использовать последовательно – два и даже бОльшее количество раз, когда бесконечно малые эквивалентные функции вложены друг в друга по принципу «матрёшек»:

Пример 10

Найти предел функции с помощью эквивалентных бесконечно малых функций

Перед решением необходимо выполнить предварительные преобразования.

В числителе вынесем за скобки «минус»: чтобы в дальнейшем воспользоваться эквивалентностью .

В знаменателе проведём искусственное преобразование , чтобы далее применить эквивалентность . Кстати, запомните это трюк с логарифмом, он используется и в других задачах математического анализа.

Начнём оформлять решение:

В числителе используем замечательную эквивалентность . В данном случае . Важнейшим моментом является тот факт, что при «икс», стремящемся к нулю, .

В знаменателе тоже бесконечно малая величина, именно поэтому можно применить эквивалентность , где при .

После замены проведена пара технических действий – вынесение «минуса» в знаменателе и сокращение минусов. Неопределённость 0:0 никуда не делась, и есть надобность воспользоваться бесконечно малыми эквивалентными функциями ещё раз. Если , то :

Задачка потолще для самостоятельного решения:

Пример 11

Найти предел функции с помощью эквивалентных бесконечно малых функций

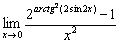
Нетрудно догадаться, что «матрёшку» следует разбирать в привычном порядке, начиная от «внешней», и заканчивая самой маленькой «внутренней». Полное решение и ответ в конце урока.

Как я уже отмечал, «икс» не обязан стремиться к нулю, он может стремиться к произвольному числу, в том числе и к бесконечности – лишь бы функции были бесконечно малыми, и существовал предел их отношений . Но практика показывает, что почти во всех заданиях , именно поэтому я и не привёл других примеров.

Тем не менее, рассмотрим более редкий тип пределов, который встречается, в частности, при исследовании числовых рядов на сходимость:

Пример 12

Найти предел функции

В данном примере «икс» стремится к бесконечности, и . Иными словами, функция бесконечно малА в точке 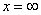. Чтобы раскрыть неопределённость целесообразно использовать теорию эквивалентных бесконечно малых величин.

Поскольку , то применима замечательная эквивалентность :

Что и говорить, вкусный способ решения.

Пример 13

Найти предел функции

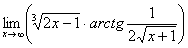
Это счастливый заключительный пример для самостоятельного решения. После эквивалентной замены неопределенность трансформируется в неопределённость , которая раскрывается по обычной схеме. Если возникли затруднения на завершающем этапе, пожалуйста, вернитесь к первой части урока Методы решения пределов.

Что тут сказать…

Всё =)

Решения и ответы:

Пример 5

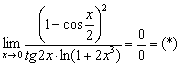
Заменим бесконечно малые функции эквивалентными функциями. При :

Пример 7

Представим логарифм в виде и заменим бесконечно малые эквивалентными. При :


Здесь числитель более высокого порядка малости, чем знаменатель.

Пример 9

Используем замечательные эквивалентности. При :

Пример 11

1) Так как , то применима эквивалентность :

2) Так как , то применима эквивалентность :

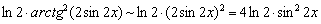
3) Так как 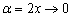, то применима эквивалентность :

Заменим бесконечно малую функцию эквивалентной:

Пример 13

Заменим бесконечно малую функцию эквивалентной функцией. Если , то .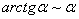

Разделим числитель и знаменатель на :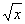

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Правила Лопиталя. Примеры решений

Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость 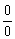или .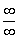

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений, Замечательные пределы. Методы решения пределов, Замечательные эквивалентности, где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.

Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.

Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.

---

Дата добавления: 2015-07-25