Замечательные пределы с экспонентой и логарифмом

На практике чаще встречаются пределы 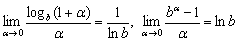и особенно их частные случаи 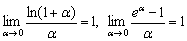. Предела 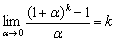лично ни разу не видел, а может быть, и видел, да не помню.

Иногда перечисленные пределы называют третьим, четвёртым и пятым замечательным пределом, но своё негативное отношение к избыточной нумерации я уже высказал на уроке Правила Лопиталя, поэтому пусть это будут «просто» замечательные пределы без номеров.

Сама техника решения мало чем отличатся от первого замечательного предела:

Пример 10

Найти предел, не пользуясь правилом Лопиталя

Чтобы использовать замечательный предел необходимо применить уже знакомый искусственный приём: в знаменателе умножаем и делим на 2:

Вот и всё. Напоминаю, что в качестве параметра «альфа» может выступать не только переменная «икс», но и сложная функция, лишь бы она стремилась к нулю. В рассмотренном примере .

Короткий закусочный предел для самостоятельного решения:

Пример 11

Найти предел, не пользуясь правилом Лопиталя

Заметьте, что условие задачи не ограничивает нас в выборе действий, примеры можно было решить и через замечательные эквивалентности:
(эквивалентность ).

(эквивалентности )

Какой способ выбрать? Рекомендую всё-таки решать через замечательные пределы (конечно, если пример не дико сложный) – выглядит солиднее.

Существенная особенность пределов 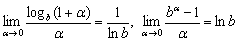состоит в том, что при перестановке числителя и знаменателя результаты тоже «переворачиваются»:

Пример 12

Найти предел, не пользуясь правилом Лопиталя

Как говорится, мал пример да заковырист….

Решаем:

На первом шаге нужно перейти к новой переменной ТАК, чтобы она стремилась к нулю.
Проведём замену: 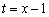, тогда:
Если , то

Для самостоятельного решения:

Пример 13

Найти предел, не пользуясь правилом Лопиталя

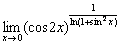
Если возникли затруднения на начальном этапе, пожалуйста, вернитесь к Примеру №9.

Разберём напоследок что-нибудь посложнее. Типовой и довольно распространённый предел:

Пример 14

Найти предел, не пользуясь правилом Лопиталя

Сначала полное решение, потом комментарии:

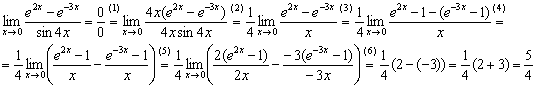
(1) На первых шагах избавляемся от синуса. Умножим числитель и знаменатель на .
(2) Используем первый замечательный предел 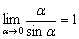, где . Константу 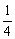выносим из предела.
(3) Проводим искусственное преобразование числителя. Возьмите его на заметку, разность экспонент раскручивается именно так.
(4) Почленно делим числитель на знаменатель.
(5) Числитель и знаменатель первой дроби умножаем на 2. Числитель и знаменатель второй дроби умножаем на –3.
(6) В обеих дробях используем замечательный предел , после чего остались от козлика рожки да ножки.

Используя правило Лопиталя, выполним проверку:

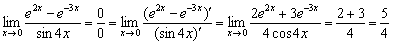
Заключительный пример посвящен раритету 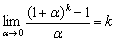. Если его не встречал я, то это не значит, что его не встретите вы. Встретите. Причём, прямо сейчас =)

Пример 15

Найти предел, не пользуясь правилом Лопиталя

Это пример для самостоятельного решения.

Всего примеров получилось таки 15-ть, а не 20-ть, и ваш покорный слуга постарался отобрать самые распространенные вещи. Желающие ознакомиться с другими пределами, могут закачать соответствующий архив решений в банке задач по высшей математике. Однако должен предупредить, будьте осторожнее – некоторые экземпляры не то, чтобы сильно сложные, но точно рождены воспалённым сознанием. Я постарался разобрать тему без навороченных нелепых примеров, поскольку убеждён, что студент должен мучиться с удовольствием =)

И приснится вам сегодня правило Лопиталя =)

Решения и ответы:

Пример 2

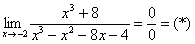
Разложим числитель и знаменатель на множители.
В числителе используем формулу суммы кубов :

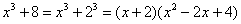
Знаменатель:

Таким образом:

Пример 4

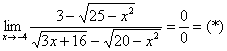
Умножим числитель и знаменатель на сопряженные выражения.

Разложим числитель и знаменатель на множители:

Пример 6

Умножим числитель и знаменатель на сопряженное выражение, используем формулу разности кубов :

Пример 8
Используем формулу :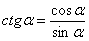

Проведём замену переменной:
Если , то

Используем тригонометрическую формулу :

Используем формулы половинного аргумента :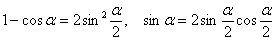

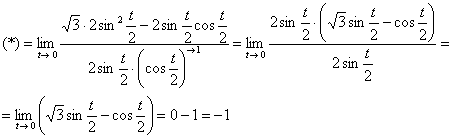
Дата добавления: 2015-07-25