Вычислить предел, используя правило Лопиталя

Для разминки разберёмся с парой небольших воробушков:

Пример 3

Вычислить предел по правилу Лопиталя

Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:

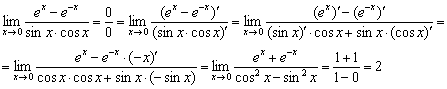
В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .

Рассмотренный пример разруливается и через замечательные пределы, похожий случай разобран в конце статьи Сложные пределы.

Пример 4

Вычислить предел по правилу Лопиталя

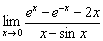
Это пример для самостоятельного решения. Нормально пошутил =)

Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:

Пример 5

Вычислить предел, используя правило Лопиталя

Напрашивается применение замечательной эквивалентности, но путь жёстко предопределён по условию:

После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения. Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.

Пример 6

Вычислить предел, используя правило Лопиталя

Пример 7

Вычислить предел, используя правило Лопиталя

Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.

И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена.

Пример 8

Вычислить предел, используя правило Лопиталя

Поехали:

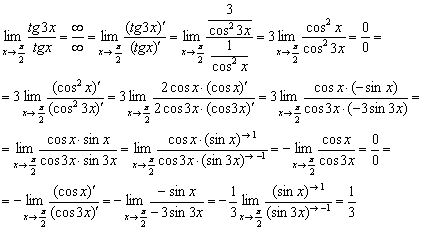
Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость 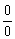, и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.

На днях мне попалось любопытное задание:

Пример 9

Вычислить предел функции, используя правило Лопиталя

Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.

Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….

В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .

Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов. Давайте для проформы ещё один:

Пример 10

Вычислить предел функции, используя правило Лопиталя

На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость 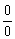. А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.

Неопределённость тоже не сопротивляется превращению в 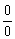или :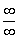

Пример 11

Вычислить предел функции с помощью правила Лопиталя

Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций. Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.

Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость 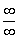, далее решение идёт по шаблонной схеме:

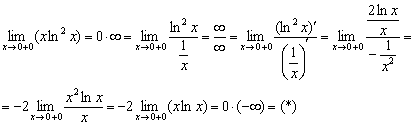
После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:

Готово.

Исходный предел можно было попытаться свести к двум бубликам:

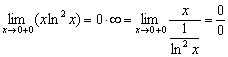
Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.

Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».

В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи 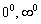. Метод трансформации прост и стандартен:

Пример 12

Вычислить предел функции с помощью правила Лопиталя

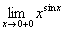
Для устранения неопределённости 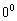используем основное логарифмическое тождество: . В данном случае :

На предпоследнем шаге, согласно известному школьному свойству, «сносим» синус из степени за пределы логарифма, получая произведение . На последнем шаге перемещаем значок предела в показатель (поскольку экспоненциальная функция непрерывна, да и предел относится, прежде всего, к верхнему этажу).

Чтобы не мельчить, вычислим предел показателя отдельно:

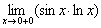
С неопределённостью разбираемся уже знакомым способом – делаем дробь трёхэтажной, получая долгожданную неопределённость , к которой применимо правило Лопиталя:

Метаморфозы продолжаются, теперь вылезла неопределённость «ноль на ноль». В принципе, можно избавиться от косинуса, указав, что он стремится к единице. Но мудрая стратегия заключается в том, чтобы никто ни до чего не докопался. Поэтому сразу применим правило Лопиталя, как этого требует условие задачи:

Не торопитесь, предел не равен нулю! Мы вычислили только предел показателя. В конце решения главное не забыть про экспоненту, я сейчас сам чуть про неё не забыл =) Окончательно:

В ряде случаев после использование основного логарифмического тождества удаётся миновать неопределённость :

Пример 13

Вычислить предел по правилу Лопиталя

Очередной папуас 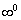тоже сдаётся перед формулой . В данном случае :

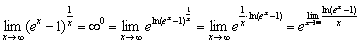
В результате сразу получена неопределённость 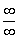, что облегчает задачу. Предел показателя для удобства вычислим отдельно:

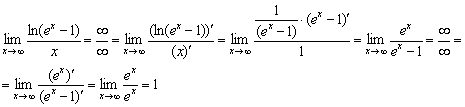
В итоге:

Аналогичное задание для самостоятельного решения:

Пример 14

Вычислить предел по правилу Лопиталя

Полное решение и ответ в конце урока.

Предел с неопределённостью по правилу Лопиталя, если честно, у себя не нашёл, но для полноты картины решим многострадальный шестой пример урока Замечательные пределы:

Пример 15

Вычислить с помощью правила Лопиталя

Решайте =)

В заключение хочу успокоить гринписовцев – ни один воробей от оружия серьёзно не пострадал, пределы – птицы юркие, да и ядра формы обтекаемой. Вспоминаем обычное требование: «…не пользуясь правилом Лопиталя». С беспощадной действительностью соприкоснёмся в статье Сложные пределы.

Желаю успехов!

Решения и ответы:

Пример 4

Пример 6

Пример 7

Пример 9

Пример 14
Используем основное логарифмическое тождество и преобразование :

Вычислим предел показателя:

Таким образом: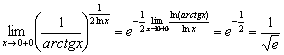

Пример 15
Используем основное логарифмическое тождество:

Вычислим предел показателя:

Таким образом:

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Сложные пределы

В данной статье будут рассмотрены пределы повышенной сложности, и заключительный практикум по теме предназначен, прежде всего, для читателей со средним и высоким уровнем подготовки. Если ваши навыки вычисления пределов невелики или вовсе отсутствуют, пожалуйста, начните с вводного урока Пределы функций. Примеры решений. Многие методы решения пределов, о которых пойдёт речь, уже знакомы и сложность будет состоять преимущественно в технике вычислений. Кроме того, мы рассмотрим примеры с более редкими замечательными пределами, которые до сей поры были обделены моим вниманием.

Пока не знаю, сколько будет примеров, 15-ть, 20-ть или больше, но в любом случае программа предстоит насыщенная, поэтому сразу приступим к зачистке территории:

Пример 1

Найти предел, не пользуясь правилом Лопиталя

При подстановке «единицы» в выражение под знаком предела, получается неопределённость 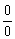, которая устраняется стандартным методом: числитель и знаменатель необходимо разложить на множители, а затем что-нибудь сократить. Разложить на множители…. Были бы у нас многочлены второй степени – без проблем. Но как раскладывать кубические многочлены? Познакомимся с новым приёмом, который основан на одной из теорем алгебры. Сначала кратко передам теоретическую суть:

Рассмотрим многочлен положительной степени. Если число является корнем уравнения , то многочлен делится на многочлен без остатка. В результате деления получается многочлен , при этом: .

Да, многочлены, как и числа, можно делить друг на друга. Термины те же:
– делимое;
– делитель;
– частное.

Начнём оформлять решение и детально разберём техническую сторону вопроса:

Разложим числитель и знаменатель на множители.

Числитель: поскольку число является корнем уравнения, то многочлен делится на многочлен без остатка. Деление выполняется столбиком. В школе столбиком мы делили числа, и принцип деления многочленов весьма похож. Записываем начальный шаблон: Обратите внимание на очень важную вещь: в многочлене в явном виде отсутствует «икс» в первой степени. При делении ОБЯЗАТЕЛЬНО прописываем все недостающие слагаемые, прикрепляя к ним нулевые коэффициенты.

Теперь в углу нужно разоблачить незнакомца :

Каким он должен быть? Девчонки, признавайтесь =) …Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :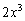

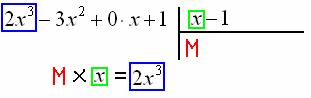
Очевидно, что данному критерию удовлетворяет . Действительно, . Записываем первый трофей:

Далее нашего героя необходимо умножить на делитель :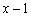
, а результат записать во второй строке слева:

Проводим отчёркивание и из первой строки почленно вычитаем вторую строку:

Если подробно, (ноль под чертой не пишем),

Сносим сверху следующее слагаемое:

Алгоритм идёт на следующий круг. Снова ищем одночлен , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :

В данном случае . Рисуем его справа под чертой:

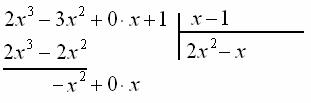
и умножаем на делитель :
, результат записываем в 4-ую строку:

Ещё раз отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем), :

Сносим сверху последнее слагаемое:

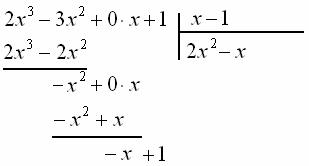
Организуем завершающий цикл. Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :

Уравнению соответствует корень , который записываем справа под чертой:

Умножаем на делитель :
, результат записываем в 6-ую строку:

Выполняем завершающее отчёркивание и почленное вычитание:

В итоге получился ноль, и это значит, что все вычисления выполнены правильно. Иными словами, многочлен поделился на 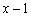без остатка. Таким образом:

Желающие могут раскрыть скобки в правой части и убедиться, что получится исходный многочлен .

Рассмотренный алгоритм на самом деле не сложен, и рука набивается довольно быстро.

Знаменатель. Разборки аналогичны. Так как число является корнем уравнения , то соответствующий многочлен делится на 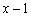без остатка:

В итоге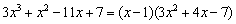

Открываем решение и записываем всё, что нажито непосильным трудом:

Приключения продолжаются – после сокращения неопределённость не устранена. Но уже легче, квадратные трёхчлены можно разложить на множители тривиальным способом, рассмотренным на первом уроке про пределы функций. Тем не менее, в целях закрепления алгоритма продолжим деление. Да простит меня сервак =)

Числитель. Поскольку число является корнем уравнения , то соответствующий многочлен делится на 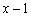без остатка. Поехали. На первом шаге подбираем ТАКИМ образом, чтобы при его умножении на «икс» получить :

Искомое значение :

Умножаем на делитель :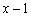
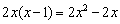, результат записываем слева, отчёркиваем и проводим почленное вычитание:

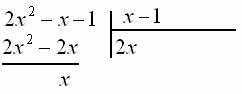
Из первой строки сносим оставшееся слагаемое:

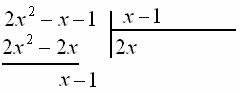
Второе значение при умножении на «икс» должно давать «икс»:

Очевидно, что :

Умножаем на делитель :
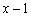, результат записываем ниже, отчёркиваем и проводим почленное вычитание:

В остатке получился ноль, значит, деление выполнено верно. Таким образом:

Аналогично расправляемся со знаменателем:

То есть

Снова открываем решение и получаем окончательный ответ:

Выполним проверку. Дважды используем правило Лопиталя:

Сравните трудоёмкость двух способов решения. Думаю, теперь вам понятно, почему запрещают применять правило Лопиталя =)

Времени и сил на первый пример совсем не жалко, так как необходимость делить многочлены время от времени возникает в других задачах, в частности, при нахождении нулей функции, в интегралах от дробно-рациональной функции. Поэтому с энтузиазмом отнесёмся к другим пределам… …они будут ещё длиннее =) Никто не знает, вдруг в жизни пригодится. Хах. Вспомнился заезженный анекдот в тему: если к вам на улице подошли Свидетели Иеговы, перехватите инициативу – начните им рассказывать про тройные интегралы.

Пример 2

Найти предел, не пользуясь правилом Лопиталя

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Вернёмся к другому известному способу решения пределов, повысив их сложность:

Пример 3

Найти предел, не пользуясь правилом Лопиталя

Неопределённость 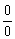ликвидируется стандартным методом – умножением и делением на сопряженное выражение. Единственное отличие, приём используется два раза:

1) для устранения разности домножаем числитель и знаменатель на сопряженное выражение ;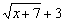

2) для устранения разности домножаем числитель и знаменатель на сопряженное выражение .

Далее дважды используется формула . Сама техника решения подробно рассмотрена на уроке Пределы. Примеры решений.

Оформляем:

Оба вышеуказанных действия выгоднее выполнить «за один присест». Умножим числитель и знаменатель на сопряженн ые выражени я:

Проверим решение по правилу Лопиталя:

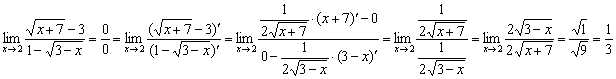
Пример 4

Найти предел, не пользуясь правилом Лопиталя

Это более сложный пример для самостоятельного решения.

Иногда в пределах рассматриваемого типа приходится использовать не только формулу разности квадратов , но и формулу разности кубов:

Пример 5

Найти предел

Неопределённость устраняется умножением и делением на сопряженное выражение. Аналогичные, но более простые пределы мы рассмотрели в Примерах №№11-13 урока Методы решения пределов. Только здесь работает формула разности кубов:

В данном случае 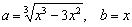. И, согласно формуле, для разности сопряженным выражением будет вот этот вот страх:

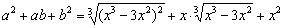
Умножим и разделим на сопряженное выражение, чтобы использовать формулу :

Тоже знакомая картина….

Старшая степень числителя: 2
Старшая степень знаменателя: 2

Таким образом, числитель и знаменатель одного порядка роста, и сразу можно сказать, что предел равен конечному числу.

Разделим числитель и знаменатель на :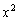

Готово.

Пример 6

Найти предел

Это пример для самостоятельного решения. После умножения/деления на сопряженное выражение и упрощений предел будет сведён к случаю Примеров №№1-3 статьи о бесконечно малых функциях. Полное решение и ответ в конце урока.

А сейчас обещанные на уроке Методы решения пределов плюшки на замену переменной. Повышенной сложности:

Пример 7

Найти предел, не пользуясь правилом Лопиталя

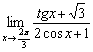
Аргумент стремится к не самому распространённому числу: , с ходу и не сообразишь, есть здесь вообще неопределённость или нет. Поэтому откроем тригонометрическую таблицу, и выпишем следующие значения:

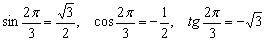
Проверим предел на наличие неопределённости:

Да, действительно, два бублика.

Проведём предварительный анализ. В пределе находятся тригонометрические функции, и решение, скорее всего, сведётся к первому замечательному пределу. В этой связи напрашивается замена, после которой новая переменная будет стремиться к нулю.

Но перед заменой целесообразно провести некоторое упрощение выражения. В пределе есть тангенс, а работать с этой функцией неудобно (как и с котангенсом тоже). Таким образом, сначала лучше свести всё дело к синусам и косинусам. Пример свирепый, поэтому я закомментирую каждый шаг:

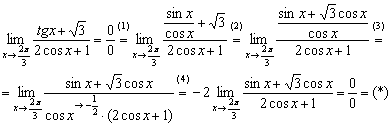
(1) Используем формулу .
(2) Дробь числителя приводим к общему знаменателю.
(3) Избавляемся от трёхэтажности дроби, а также от косинуса, указывая, что .
(4) Выносим константу за значок предела.

Неопределённость никуда не делась, но от тангенса мы избавились, что уже является небольшим достижением

Проведем замену переменной:
Если , то
Ну и ещё – из замены нужно выразить: .

(5) Выполняем подстановку в соответствии с выполненной заменой.
(6) Используем тригонометрические формулы:

(7) Используя значения , упрощаем выражение.
(8) Раскрываем скобки в числителе и знаменателе.
(9) Приводим подобные слагаемые в числителе.
(10) Константу –2 выносим за значок предела. В знаменателе переставляем слагаемые.

И снова два нуля, причём не видно как решать предел дальше…. Но если хорошенько пошуршать в тригонометрических формулах, то история закончится счастливым концом:

(11) Используем формулы половинного угла: . В числителе избавляемся от косинуса, указывая, что .
(12) В знаменателе выносим за скобки .
(13) Сокращаем числитель и знаменатель на .

Забавно, что всё обошлось даже без замечательного предела.

Не знаю, кто и на каком месте будет рвать себе волосы, но правило Лопиталя даёт ответ фантастически быстро:

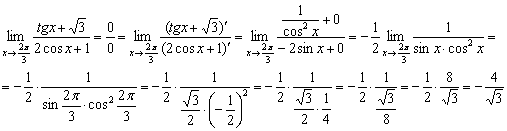
Пример 8

Найти предел, не пользуясь правилом Лопиталя

Это пример для самостоятельного решения. В тригонометрической таблице нет информации об отрицательных значениях угла. Понятие ориентации угла дано в статье Простейшие задачи с прямой на плоскости. Наглядная иллюстрация с конкретными примерами также фигурирует при нахождении аргумента комплексного числа. Чтобы воспользоваться таблицей, прибавляем один «оборот»: , то есть и 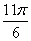– это один и тот же угол. Таким образом:

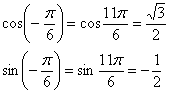
Полное решение и ответ в конце урока

Как-то незаслуженно оказались забыты степени:

Пример 9

Найти предел

На повестке дня неопределённость , и решение, очевидно, нужно свести к замечательной формуле . Но в нашем пределе нет единицы, только одинокий косинус. Что делать? Организуем!

(1) Приводим основание степени к виду , для этого используем искусственный приём: прибавляем и вычитаем единицу. Таким образом:
(2) В целях применения 2-го замечательного предела возводим основание в степень , и, чтобы ничего не изменилось – в обратную степень .
(3) Используем замечательный предел .
(4) Теперь в показателе необходимо устранить неопределённость 0:0. Сначала меняем знак в числителе: 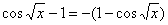, минус выносим из предела.
(5) В числителе используем формулу .
(6) Искусственно преобразуем знаменатель, чтобы получить два первых замечательных предела.

Очень кстати в одном примере подвернулись сразу оба замечательных предела, и после их повторения во второй части статьи рассмотрим:

Дата добавления: 2015-07-25