|
Читайте также: |
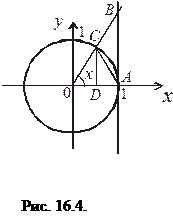
16.3.1. Первый замечательный предел:
 |
 |
. Это вытекает из неравенства 
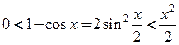и теоремы 16.3. Заметим, что 
, 
, а площадь 
меньше площади сектора 
, а та, в свою очередь, меньше площади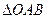 
, поэтому 
, т.е. 
при 
(см. рис. 16.4). Разделив это неравенство на 
, получим
,
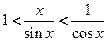Окончательно получаем: 
. В силу четности этого неравенства оно справедливо и при 
. По теореме 16.3 мы получим,
при 
.
Дата добавления: 2015-07-20; просмотров: 82 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные теоремы о пределах функций. | | | Второй замечательный предел. |