Односторонние и бесконечные производные.

При определении производной функции y=f (x) в точке х ₀ мы считаем, что функция определена в двусторонней окрестности точки х ₀ (см. рис. 18.6), а производная есть конечный предел отношения

= (18.16)

при условии, что x → x ₀ (т.е. при D х →0). Заметим, что аргумент х стремится к точке х ₀ произвольным образом.

Может случиться, что функция не дифференцируема в точке х ₀, т.е. не существует предел отношения (18.16), но могут существовать односторонние пределы этого отношения при
х → х ₀ - 0 (т.е. при D х → -0) или при х → х ₀ + 0 (т.е. при D х → +0). Это может случиться, в частности, если функция определена в односторонней окрестности точки х ₀ (только слева или только справа от точки х ₀, см. рис. 18.6).

Левой производной функции y=f (x) в точке х ₀ называется число

(x ₀)= = , (18.17)

если этот предел существует и конечен.

Правой производной функции y=f (x) в точке х ₀ называется число

(x ₀)= = , (18.18)

если этот предел существует и конечен.

Аналогично, тому, как это было сделано в пункте 18.7., можно определить односторонние касательные, для которых производные будут угловыми коэффициентами.

Если функция y=f (x) имеет в точке х ₀ производную, то она имеет в этой точке правую и левую производные, которые равны между собой.

Пример 18.13. Найти односторонние производные функции у= |sin x | в точке х ₀= 0.

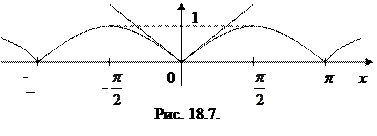Решение. Пусть х Î , тогда

|sin x |=

Заметим что D х = х-х ₀ = х.

Тогда при х Î имеем

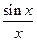D у= |sin x |-|sin 0|=sin x и (0)= = =1.

При х Î имеем D у= |sin x |-|sin 0| = -sin x и (0)= = = -1.

В точке х ₀ = 0 существуют односторонние касательные: левая у = -х и правая у = х (см. рис. 18.7)

Пусть функция y = f (x) определена в некоторой окрестности точки х ₀

Говорим, что функция y = f (x) имеет в точке х ₀ бесконечную положительную производную (пишем: f¢ (x ₀) = +¥), если =+¥,

и бесконечную отрицательную производную (f¢ (x ₀) = -¥), если = -¥.

Тогда в точке х ₀ существует вертикальная касательная с уравнением х = х ₀(см. рис. 18.8).

Аналогично определяются односторонние бесконечные производные (см. рис. 18.9)

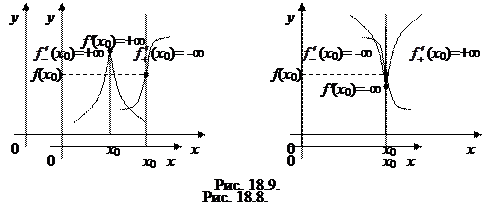Пример 18.14. Рассмотрим функцию у= в точке х ₀ =0 (см. рис. 18.10). Тогда

D у= D у (0,D х)=

и

.

Тогда функция y=f (x) имеет в точке х ₀=0 положительную бесконечную производную

f¢ (0) = = = +¥,

а х ₀ = 0 – уравнение вертикальной асимптоты.

Пример 18.15. Пусть у= и х ₀ = 0. Тогда

D у= D у (0,D х)=

и

= .

Тогда существуют односторонние бесконечные производные в точке х ₀=0. Действительно

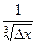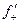(0)= = = -¥

(0)= = = +¥

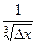а прямая х= 0 – вертикальная односторонняя касательная (см. рис. 18.11).

Дата добавления: 2015-07-20