
Читайте также:
|
Пусть функция y=f (x) определена в некоторой окрестности (х 0-d, х 0+d) точки х 0 (включая саму точку х 0).
 Придадим аргументу х в точке х 0 произвольное приращение D х такое, что точка х=x 0+D х Î (х 0-d, х 0+d). Тогда функция y=f (x) получит приращение D у= f (x) - f (x 0)= f (x 0+D х) - f (x 0) (см. рис. 18.1).
Придадим аргументу х в точке х 0 произвольное приращение D х такое, что точка х=x 0+D х Î (х 0-d, х 0+d). Тогда функция y=f (x) получит приращение D у= f (x) - f (x 0)= f (x 0+D х) - f (x 0) (см. рис. 18.1).
Дадим одно из важнейших понятий математического анализа: понятие производной.
Производной функции y=f (x) в точке х 0 называется предел отношения приращения функции в этой точке к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, (при условии, что этот предел существует).
Производную функцию y=f (x) в точке х 0 обозначают одним из символов:
 (x 0),
(x 0),  (x 0),
(x 0), 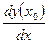 ,
,  .
.
Итак, по определению
|
(18.1)
или короче
|
(18.2)
Рассмотрим некоторые важные примеры.
Пример 18.1. y=f (x) = с – постоянная функция (с= const). Тогда для любого значения аргумента х=х 0 найдем D у = f (x 0+D х) – f (x 0)= с - с =0 для любого приращения аргумента D х, поэтому
 =
= 
 =
= 
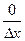 =0,
=0,
т.е. производная постоянной функции равна нулю в каждой точке числовой оси. Таким образом,  =0 (производная константы равна нулю).
=0 (производная константы равна нулю).
Пример 18.2. y=f (x)=sin x.
Так как D у = sin (x+ D x)-sin x =2 sin  cos
cos 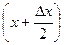 , где sin
, где sin  – б.м. при D х →0,
– б.м. при D х →0,
sin 
 , а функция у= cos x непрерывна:
, а функция у= cos x непрерывна:  cos
cos 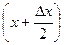 = cos x, то
= cos x, то
 (x)=
(x)= 
 =
= 
 =
= 

 cos
cos 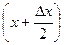 =cos x.
=cos x.
|
(18.3)
Пример 18.3. y=f (x)= ах, a >0, а ≠1.
Напомним, что ех -1 х, отсюда следует, что
 ах -1= ех ln a -1 х ln a. Тогда
ах -1= ех ln a -1 х ln a. Тогда

D у=ах+ D х - ах = ах (а D х -1) ах •D х ln а.
 Отсюда
Отсюда
у¢ =  .
.
|
|
и (18.4)
Последняя формула показывает замечательное свойство числа е: показательная функция с основанием е имеет производную, совпадающую с самой функцией. Этим объясняется преимущественное использование числа е в качестве основания степени и основания логарифмов (натуральные логарифмы).
Пример 18.4. у= f (x) = log ax, а >0, a ≠1, x >0.

 Напомним, что ln(1+ x) x и log a (1+ x)
Напомним, что ln(1+ x) x и log a (1+ x) 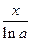 .
.
Тогда
 D у= log a (x +D x)-log ax =log a
D у= log a (x +D x)-log ax =log a 
 ,
,
откуда получаем
 =
= 
 =
= 
 =
= 
 =
=  .
.
Итак,
|
и (18.5)
Пример 18.5. y = f (x) = xn, n – натуральное число.
Используя правило возведения бинома в степень (см. формулу бинома Ньютона (13.2)), имеем D у= (х+ D х)п-хп = п хп-1 D х+  хп-2 D х2+... + D хп,
хп-2 D х2+... + D хп,
откуда при D х ¹ 0 получим  .
.
При D х® 0 все слагаемые правой части, содержащие множитель D х в степени с натуральным показателем, стремятся к нулю, то

 =
= 
 =
= 

Таким образом,
|
|
|
|
Дата добавления: 2015-07-20; просмотров: 56 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Свойства функций, непрерывных на отрезке. | | | Дифференцируемость. |