Локальные свойства непрерывных функций.

Локальные свойства функции – это такие свойства, которые выполняются в данной точке или в некоторой окрестности этой точки. Примером локального свойства функции служит свойство функции быть непрерывной в данной точке.

Теорема 17.1. (Арифметические свойства непрерывных функций).

Пусть функции f (x) и g (x) непрерывны в точке х₀. Тогда их сумма f (x) + g (x), произведение f (x) g (x) и частное 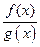также непрерывны в точке х₀ (последняя при g (x)¹ 0).

Доказательство. Так как f (x) и g (x) непрерывны в точке х₀, то существуют пределы 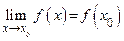и 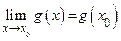. Тогда

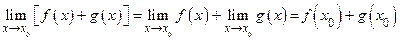, где f (x₀) + g (x₀) – значение функции f (x) + g (x) в точке х₀. Это и означает, что сумма непрерывных в точке х₀ функций также непрерывна в точке х_0. Непрерывность произведения и частного двух функций доказывается аналогично.

Теорема 17.2. (О непрерывности сложной функции).

Пусть функция у = f (x) непрерывна в точке х₀, а функция z = g (x) непрерывна в точке y₀ = f (x₀). Тогда сложная функция z = F (x) = g [ f (x) ] непрерывна в точке х₀.

Доказательство. Функция у=f(x) непрерывна в точке х₀, т.е. 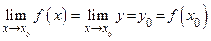, т.е. у = f (x)® у₀ = f (x₀) при х® х₀. Так как z = g (y) непрерывна

в точке у₀, то 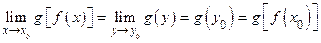, это и означает, что сложная функция g [ f (x) ] непрерывна в точке х₀.

Пример 17.1. Рассмотрим функцию у = f (x)=U(x)^V(x), U(x) >0, U(x), V(x) непрерывны в точке х₀: $ 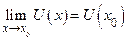и $ . Эта функция у = U^V сложная, она одновременно показательная и степенная. По теореме 17.2 эта функция непрерывна в точке х₀:

.

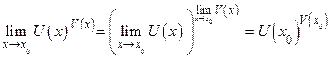Как мы видели (см. п. 16.2), при рассмотрении пределов вида 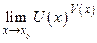могут возникнуть неопределенности вида 0⁰, 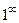или 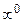. Методы их вычисления будут рассмотрены ниже.

Функция у = f (x) называется непрерывной слева в точке х₀, если f (x₀ – 0) = = 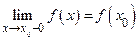, и непрерывной справа в точке х₀, если f (x₀ + 0) = .

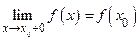Дата добавления: 2015-07-20