Основные свойства б.м. функций.

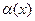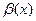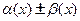1) Сумма бесконечно малых функций есть бесконечно малая функция, т.е. если , - б.м. функции при , то - б.м. функция при .

Следствие: Сумма конечного числа б.м. функций есть б.м. функция.

Это непосредственно вытекает из определения 1 предела функции и соответствующего свойства б.м. последовательностей (см. пункт 14.5, свойство 1).

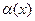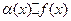2) Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая, т.е. если функция ограничена в окрестности точки , а - б.м. при , то - б.м. функция при .

Это вытекает из определения 1 предела функции и свойств б.м. последовательностей (см. пункт 14.5, свойство 2).

Следствия: а) Произведение б.м. функции на число есть б.м. функция;

б) Произведение б.м. функции есть б.м. функция;

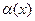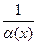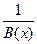в) Связь б.м. б.б. функций: обратная к б.м. функции есть б.б. функция и наоборот, т.е. если - б.м. функция при и , то функция - б.б. функция при . Обратно, если б.б. функция при , то - б.м. функция при .

Вытекает из определения 1 предела функции и аналогичного свойства предела последовательности.

Пример 16.10. Вычислить 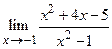(см. пример 16.8).

Функция f (x) = x ² + 4 x – 5 имеет предел в точке х ₀ = -1: 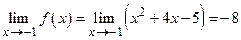, а функция g (х) = х ² –1 есть б. м. при х ® -1, тогда обратная к ней функция 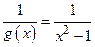– б. б. при х ® -1, следовательно

.

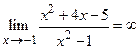Дата добавления: 2015-07-20