Дифференцируемость.

Функция y=f (x) называется дифференцируемой в точке х ₀, если ее приращение D у в этой точке можно представить в виде

(18.7)

D у=А• D х+ (D х)= А• D х+α (D х)•D х  

,

где А – некоторое число, α (D х) – б.м. при D х →0, т.е. α (D х)=0, а (D х) – б.м. при D х →0 более высокого порядка, чем D х; т.е. 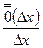=0.

Связь между дифференцируемостью функции в точке и существованием производной в той же точке дает следующая теорема.

Теорема 18.1. Функция y=f (x) дифференцируема в точке х ₀ тогда и только тогда, когда она имеет в этой точке конечную производную f¢ (x ₀).

Доказательство. Необходимость. Пусть функция y=f (x) дифференцируема в точке х ₀, т.е. D у=А• D+ α (D x)•D x. Тогда при х →0 существует предел

= (А+α (D х))= А= f¢ (x ₀),

т.е. производная в точке х ₀ существует и f¢ (x ₀)= А.

Достаточность. Пусть существует производная f¢ (x ₀), т.е. существует предел = f¢ (x ₀). Тогда, согласно теореме 16.4., справедливо представление

= f¢ (x ₀)+ α (D х) или D у=f¢ (x ₀)D х+α (D х)•D х,

где α (D х) - б.м.при D х →0. последнее равенство и означает, что функция y=f (x) дифференцируема в точке х ₀.

Вывод: для функций одной переменной дифференцируемость и существование производной – понятия равносильные. При этом формулу (18.7) можно записать в виде

D у= f¢ (x ₀)D х + (D х), (18.8)

а операцию нахождения производной называют дифференцированием функции.

Из формулы (18.8) вытекает, что

1) если f¢ (x ₀)≠0, то приращение функции D у является б. м. первого порядка относительно D х →0;

2) если f¢ (x ₀)=0, то D у = (D х), т.е. является б. м. более высокого порядка, чем D х →0.

Связь между дифференцируемостью и непрерывностью функции в точке:

если функция y=f (x) дифференцируема в точке х ₀, то она и непрерывна в этой точке.

Действительно, если y=f (x) дифференцируема в точке х ₀, то ее приращение имеет вид (см. формулу (18.8))

D у= f¢ (x ₀)D х + α (D х)•D х =[ f¢ (x ₀)+ α (D х)]•D х

и является б. м. при D х →0 (как произведение б. м. функции D х →0 на ограниченную в окрестности точки х ₀ функцию f¢ (x ₀)+ α (D х), где α (D х) – б.м. при D х →0). Таким образом, D у =0, что равносильно непрерывности функции y=f (x) в точке х ₀ (см. п. 17.1).

Замечание. Обратное утверждение не верно. Из непрерывности функции в точке, вообще говоря, не следует ее дифференцируемость в этой точке (см. пример 18.6).

Пример 18.6. y=f (x)= непрерывна на всей числовой оси, включая точку х ₀=0. Покажем, что эта функция не имеет производной в точке х ₀. Действительно,

D у= D у (0,D х)= - = ,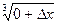

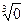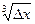тогда

= = =+¥.

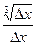это и означает, что функция у= не дифференцируема в точке х ₀, хотя и непрерывна в этой точке. Заметим, что D у = 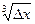= 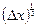есть б. м. порядка 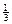<1 по отношению к D х →0 (см. выводы из теоремы 18.1).

Дата добавления: 2015-07-20