Точки разрыва функции и их классификация.

Пусть функция у = f (x) определена в некоторой окрестности точки х₀, включая саму точку х₀.

Сформулируем одно важное для дальнейшего утверждение: функция у = f (x) непрерывна в точке х₀ тогда и только тогда, когда 1) функция определена в точке х₀, т. е. существует значение функции f (x₀), 2) существуют предел слева f (x₀ –0) и предел справа f (x₀ +0) функции у = f (x) в точке х₀, 3) все эти три числа равны между собой: f (x₀ –0) = f (x) = f (x₀ +0).

Геометрически это ясно (см. рис. 17.3). Нарушение одного из этих трех условий означает, что функция уже не является непрерывной в этой точке.

Точки, в которых нарушается непрерывность функции, называются точками разрыва функции.

Классификация точек разрыва функции.

1. Точка х = х₀ называется точкой устранимого разрыва функции у = f (x), если существуют односторонние пределы f (x₀ –0) и f (x₀ +0), которые равны между собой:
f (x₀ –0) = f (x₀ +0), но либо функция f (x) не определена в точке х₀ (см. рис. 17.4а), либо функция определена в точке х₀, т. е. существует ее значение f (x₀) в этой точке, не равное односторонним пределам: f (x₀ ±0) ¹ f (x₀) (см. рис. 17.4б).

Пример 17.2. Рассмотрим функцию , определенную и непрерывную в каждой точке числовой прямой, кроме точки х₀ = 4, которая является точкой разрыва функции. Ясно, что y = f (x) = x-1 при x ¹ 4. Поэтому существует предел нашей функции в точке х₀ = 4: 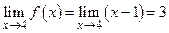, т.е. существуют односторонние пределы f (4 ±0) и они равны между собой: f (4 - 0) =3 = f (4+0) (см. рис. 17.5). Это означает, что х₀ = 4 – точка устранимого разрыва.

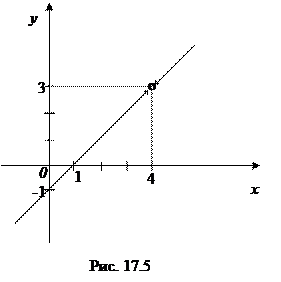Заметим еще раз, что функция при x ¹ 4 совпадает с непрерывной всюду функцией y = f₁ (x) = x- 1. Доопределив нашу функцию в точке х = 4 условием f ( 4 ) = 3, мы получим непрерывную в точке х₀ = 4 функцию

, т.е. устранили разрыв.

2. Точка х = х₀ называется точкой разрыва первого рода (или скачком) функции y = f (x), если в точке х₀ существуют односторонние пределы f (x₀ -0) и f (x₀ +0), которые не равны между собой: f (x₀ -0) ¹ f (x₀ +0) (см. рис. 17.6). При этом функция y = f (x) может быть определена в точке х_{0 ,} а может быть не определена.

Число h = h (x₀) = f (x₀ +0) - f (x₀ -0) называется скачком функции y = f (x) в точке х₀. Скачок может быть как положительным, так и отрицательным.

Пример 17.3. Функция y = f (x) = определена и непрерывна всюду, кроме точки х₀ = 0, которая является точкой разрыва функции. Так как то y = f (x) = =

График этой функции изображен на рис. 17.7. Точка х₀= 0 является точкой разрыва первого рода, т. е. скачком. Действительно,

т.е. f (-0) ¹ f (+0). Скачок функции в точке х₀= 0 равен h = h ( 0 ) = f (+ 0 ) - f (- 0 ) = -2.

3. Точка х = х₀ называется точкой разрыва второго рода функции y = f (x), если хотя бы один из односторонних пределов (слева или справа) не существует или равен бесконечности.

Пример 17.4. Функция y = f (x)= определена и непрерывна всюду, кроме точки х₀ = 0, которая является точкой разрыва второго рода, т.к.

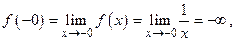
т.е. оба односторонних предела бесконечные (см. рис. 17.8).

Пример 17.5. Функция y = sin определена и непрерывна всюду, кроме точки х₀ = 0, которая является точкой разрыва второго рода, т.к. односторонние пределы в точке х₀ = 0, как показывает пример 16.3, не существуют (ни конечные, ни бесконечные).

Дата добавления: 2015-07-20