Производная сложной функции

Пусть функция y=f (x) дифференцируема в точке х ₀, а функция z=g (y)дифференцируема в точке y ₀ =f (x ₀). Тогда сложная функция z=F (x)= g [ f (x)] дифференцируема в точке х ₀ и справедлива формула (правило дифференцирования сложной функции)

F¢ (x ₀)= g¢ (y ₀)• f¢ (x ₀) =g¢ [ f (x ₀)]• f¢ (x ₀).

Действительно, функция y=f (x) дифференцируема в точке х ₀, поэтому

D у = f¢ (x ₀)•D х+α (D х)•D х, (18.9)

где α (D х) – б.м. при D х →0, а в силу непрерывности функции y = f (x) в точке х ₀ имеем D у →0, т.е. D у – б. м. при D х →0.

Далее, функция z = g (y) дифференцируема в точке y ₀ =f (x ₀) поэтому

D z = D F = g¢ (y ₀)D y+β (D y)•D х, (18.10)

где β (D y) – б. м. при D у →0. Учитывая, что приращение D у зависит от D х, то функция β (D y) зависит от D х как сложная функция β (D у) – б. м. при D х →0.

Подставим представление (18.9) в формулу (18.10), получим

D z= [ g¢ (y ₀)• f¢ (x ₀)]D x+ [ g¢ (y ₀) α (D х)+ f¢ (x ₀) β (D y)+ α (D х) β (D y)]•D x,

где функция g(D х)= g¢ (y ₀) α (D х)+ f¢ (x ₀) β (D y)+ α (D х) β (D y) есть б. м. функция при D х →0 как сумма трех б. м. функций. Поэтому последнее равенство примет вид

D z = D F= [ g¢ (y ₀)• f¢ (x ₀)]D x +g(D x)•D x,

но это и означает, что сложная функция F (D x) = g [ f (x)] дифференцируема в точке х ₀ и F¢ (x ₀)= g¢ (y ₀)• f¢ (x ₀).

Сформулируем правило нахождения производной сложной функции z = g [ f (x)], где z = g (y) и y=f (x) (в этом случае переменную у называют промежуточной переменной). Производная сложной функции g [ f (x)] равна производной g¢ (y ₀) функции g (y) по промежуточной переменной у, умноженной на производную промежуточной переменной y¢=f¢ (x) по независимому аргументу х:

(g [ f (x)])¢= g¢ (y)• у¢=g¢ (y ₀)• f¢ (x ₀)

(18.11)

Кратко это можно выразить так:

Производная сложной функции равна произведению производных от функций, ее составляющих.

Пример 18.8. Найдем производную сложной функции у= 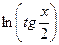, где y= ln u, u=tg v, v= . Тогда y¢ (x)= y¢ (u)• u¢ (v)• v¢ (x)=

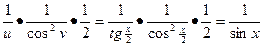
В дальнейшем при дифференцировании сложной функции не будем явно выписывать промежуточные переменные.

(cos x)¢=-sin x

Пример 18.9.

Действительно, y = cos x = sin , поэтому

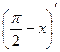у¢ = cos • =cos •(-1) = -sin x.

Дата добавления: 2015-07-20