Читайте также:
|
Вариант А
Вычислить пределы:
1. 
Ответ: 
2. 
Ответ: 
3. 
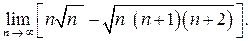Ответ: 
4. 
Ответ: 
5. 
Ответ: 
6. 
Ответ: 
7. 
Ответ: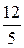 
8. 
Ответ: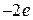 
9. 
Ответ: 
10. 
Ответ: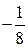 
11. 
Ответ:
12. 
Ответ: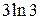 
13. 
Ответ: 
14. 
Ответ: 
15. 
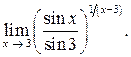Ответ: 
16. 
Ответ: 
17. 
Ответ: 
18. 
. Ответ:
19. 
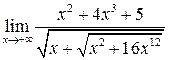. Ответ: 
20. 
. Ответ: 
21. 
. Ответ: 
22. 
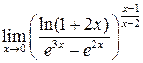. Ответ: 
23. 
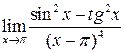. Ответ:
Вариант Б
Вычислить пределы:
1. 
Ответ:
2. 
Ответ:
3. 
Ответ: 
4. 
Ответ: 
5. 
Ответ: 
6. 
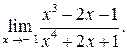Ответ: 
7. 
Ответ:
8. 
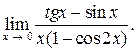Ответ: 
9. 
Ответ:
10. 
Ответ: 
11. 
Ответ: 
12. 
Ответ: 
13. 
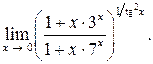Ответ: 
14. 
Ответ:
15. 
Ответ: 
16. 
Ответ:
17. 
Ответ: 
18. 
. Ответ: 
19. 
. Ответ:
20. 
. Ответ:
21. 
. Ответ: 
22. 
. Ответ: 
23. 
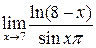. Ответ: 
Вариант В
Вычислить пределы:
1. 
Ответ:
2. 
. Ответ: 
3. 
Ответ: 
4. 
Ответ:
5. 
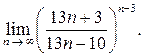Ответ: 
6. 
Ответ:
7. 
Ответ:
8. 
Ответ:
9. 
Ответ: 
10. 
Ответ: 
11. 
Ответ:
12. 
Ответ: 
13. 
Ответ: 
14. 
Ответ:
15. 
Ответ:
16. 
Ответ:
17. 
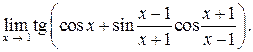Ответ: 
18. 
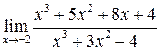. Ответ:
19. 
. Ответ:
20. 
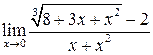. Ответ:
21. 
. Ответ:
22. 
. Ответ: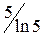 
23. 
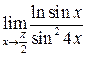. Ответ: 
Вариант Г
Вычислить пределы:
1. 
Ответ:
2. 
Ответ:
3. 
Ответ:
4. 
Ответ: 
5. 
Ответ: 
6. 
Ответ: 
7. 
Ответ:
8. 
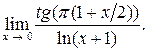Ответ: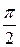 
9. 
Ответ: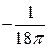 
10. 
Ответ: 
11. 
Ответ:
12. 
Ответ:
13. 
Ответ: 
14. 
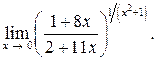Ответ: 
15. 
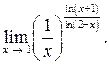Ответ:
16. 
Ответ:
17. 
Ответ:
18. 
. Ответ:
19. 
. Ответ: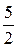 
20. 
. Ответ:
21. 
. Ответ: 
22. 
. Ответ:
23. 
. Ответ: 
Вариант Д
Вычислить пределы:
1. 
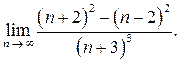Ответ:
2. 
Ответ:
3. 
Ответ:
4. 
Ответ:
5. 
Ответ:
6. 
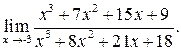Ответ:
7. 
Ответ:
8. 
Ответ: 
9. 
Ответ: 
10. 
Ответ: 
11. 
Ответ: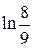 
12. 
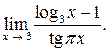Ответ: 
13. 
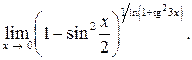Ответ: 
14. 
Ответ: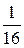 
15. 
Ответ:
16. 
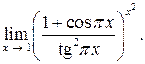Ответ:
17. 
Ответ: 
18. 
. Ответ: 
19. 
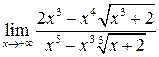. Ответ:
20. 
. Ответ:
21. 
. Ответ: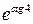 
22. 
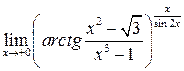. Ответ: 
23. 
. Ответ:
Решение задач на пределы.
1. Вычислить пределы функций.
а) Найти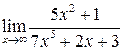 
.
Решение. Прежде всего, проверим, применимы ли к данной дроби теоремы о пределах, или мы имеем дело с неопределенностью. Для этого найдем пределы числителя и знаменателя дроби. Функции 
и 
являются бесконечно большими. Поэтому,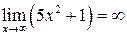 
, 
.
Следовательно, имеем дело с неопределенностью вида 
.
Для раскрытия этой неопределенности и использовании теоремы о пределе отношения двух функций выделим в числителе и в знаменателе 
в старшей для числителя и знаменателя степени в качестве сомножителя и сократим дробь.
Дата добавления: 2015-07-25; просмотров: 41 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Тема 10. Перспективные направления развития методики | | | Ответ. . |