Неявное задание функции и ее дифференцирование.

Пусть задано уравнение, связывающее переменные х и у, вида

F (x, y) = 0. (18.30)

Мы уже сталкивались с подобным уравнением, рассматривая уравнение линии на плоскости в п. 7.1.

Пусть существует такой интервал (a, b), что для каждого x₀ Î (a, b) существует по крайней мере одно число у, удовлетворяющее уравнению F (x, y) = 0. Обозначим одно из таких чисел у₀ и поставим его в соответствие числу x₀ Î (a, b). Тогда получим функцию y = f (x), определенную в интервале (a, b) и такую, что F (x, f (x)) = 0 для всех x Î (a, b). В этом случае говорим, что функция y = f (x) задается неявно уравнением (18.30). Уравнение (18.30) задает, вообще говоря, не одну, а некоторое множество функций.

Функции, неявно задаваемые уравнениями вида (18.30), называются неявными функциями

в отличие от функций, задаваемых явно формулой y = f (x). Термин " неявная функция" отражает

не характер функциональной зависимости, а лишь способ ее задания.

Итак, функция y = f (x), x Î (a, b) является неявной функцией, определяемой уравнением (18.30), если

F (x, f (x)) º 0 " x Î (a, b),

т.е. функция y = f (x) есть решение уравнения F (x, y) = 0 относительно переменной y.

Пример 18.19. Рассмотрим уравнение х² + у² – 1 = 0, или х² + у² = 1, которое на плоскости Оху задает окружность радиуса r = 1 с центром в начале координат (см. рис. 18.16). Как легко
проверить, функции , x Î [ - 1, 1] и , x Î [ - 1, 1] являются неявными функциями, заданными этим уравнением, графиками их служат верхняя и нижняя полуокружности (см. рис. 18.6).

Выберем x₀ = 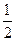Î [ - 1, 1] и подставим в исходное уравнение. Тогда получим: + у² – – 1 = 0 или у² = , т.е. y = . Итак, при
x₀ = 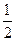мы получили два значения у. Если мы выберем у₀ = 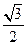; то, тем самым, мы выбрали неявную функцию , x Î [ - 1, 1].

Правило нахождения производных функций, заданных неявно.

Для нахождения производной y¢ функции y = f (x), заданной неявно уравнением F (x, y) = 0, необходимо продифференцировать это уравнение по переменной x как сложную функцию, рассматривая при этом y как функцию от x, и полученное уравнение разрешить относительно y¢.

Производная неявной функции выражается через аргумент х и функцию у, т.е. сама является функцией, заданной неявно.

Пример 18.20. Найти y¢ (1) и y¢¢ (1) в точке М₀ (1,1), если y = f (x) является неявной функцией, определяемой уравнением х² + 2 ху + у² – 4 х + 2 у -2 = 0 (18.31) Решение. Продифференцируем уравнение (18.31) по х, помня, что у есть функция от х:

2 х + 2(у +ху¢) + 2 уу¢ - 4 + 2 у¢ = 0.

Находя из этого уравнения у¢, получим

. (18.32)

Чтобы вычислить y¢ (1), нам необходимо знать значение у₀ неявной функции в точке x₀ = 1. Но из условия задачи следует, что у₀ = y (1) = 1, т. к. точка М₀ (1,1) лежит на графике функции. Учитывая это, получим: y¢ (1) = 0.

Для нахождения y¢¢, продифференцируем уравнение (18.32) еще раз по переменной x:

.

Исключив из последнего равенства y¢ по формуле (18.32), получим выражение y¢¢ через х и у: 1 + y¢ = 1 – ,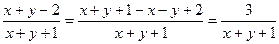

тогда y¢¢ = .

Отсюда, учитывая как и выше, что y (1) = 1, получим y¢¢ (1) = – .

Замечание. Задав точку М₀ (1,1), лежащую на кривой, определенной уравнением (18.31) (проверьте), мы тем самым, задали значение неявной функции y = f (x) в точке x₀ = 1: y (1) = 1. Дело в том, что уравнение (18.31) при x₀ = 1 имеет два решения: у = 1 и у = -5. Уравнение (18.31) можно разрешить относительно y, записав его в виде у² + 2(х + 1) у + х² – 4 х – 2 = 0, откуда получим: y = f₁ (x) = – х – 1 + 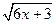и y = f₂ (x) = – х – 1 – 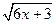. Легко видеть, что
f₁ (x) = 1, а f₂ (x) = –5. Решить поставленную задачу можно теперь, дифференцируя функцию
y = f₁ (x), заданную уже в явном виде.

Это замечание показывает, что даже в случае, когда уравнение, задающее неявную функцию, можно разрешить относительно у, производную неявной функции проще находить по правилу, описанному выше.

18.13. Основные теоремы дифференциального исчисления.

Теорема 18.3 (Теорема Ферма). Пусть функция y = f (x) определена в некоторой окрестности точки x₀ и принимает в этой точке наибольшее или наименьшее значение. Тогда, если в точке x₀ существует производная, то она равна нулю, т. е. f ¢ (x₀) = 0.

Доказательство. Пусть для определенности функция y = f (x) в точке x₀ принимает наибольшее значение, т. е. f (x) £ f (x₀) для любого x Î (х₀ -d, х₀ -d) (см. рис. 18.17). Ясно, что

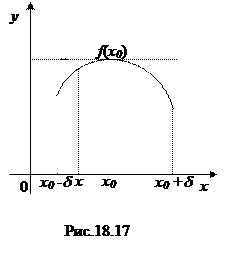D у = f (x) – f (x₀) £ 0 для любого x Î (х₀ -d, х₀ -d).

Если x > x₀, т. е. D x = x- x₀ > 0, то и, следовательно,. f ¢ (x₀) = = £ 0.

Если x < 0, т. е. D x < 0, то и, следовательно,

f ¢ (x₀) = = ³ 0.

Но это возможно только тогда, когда f ¢ (x₀) = 0.
Аналогично рассматривается случай, когда в точке x₀ функция y = f (x) имеет наименьшее значение (D у ³ 0).
Доказательство теоремы Ферма закончено.

Геометрический смысл теоремы Ферма: если в точке x₀ дифференцируемая функция y = f (x) имеет наибольшее (наименьшее) значение, то в точке
(x₀ , f (x₀))касательная к графику функции y = f (x) параллельна оси Ох, т. е. горизонтальна (см. рис. 18.17).

Теорема 18.4 (Теорема Ролля). Пусть функция y = f (x):
1) непрерывна на отрезке [ a, b ];

2) дифференцируема в каждой точке интервала (a, b);
3) f (а) = f (b), т. е. на концах отрезка принимает равные значения.
Тогда существует хотя бы одна такая точка с Î (a, b), что. f ¢ (с) = 0.

Доказательство. Функция, непрерывная на отрезке, принимает наибольшее М и наименьшее т значения, т. е. существуют точки x₁ , x₂ Î [ a, b ] такие, что f (x₁) = т и f (x₂) = М и выполняются неравенства

т £ f (x₀) £ М " x Î [ a, b ].

Возможны два случая: 1) т = М; 2) т < М.
1) В этом случае f (x) = т = М = const. Поэтому. f¢ (x) = 0 в каждой точке интервала (a, b). В качестве точки с можно взять любую точку интервала (a, b).
2) В этом случае (т < М), учитывая, что f (а) = f (b), либо x₁ Î (a, b), либо x₂ Î (a, b), т. е. одно из значений т или М принимается внутри интервала (a, b). Таким образом, существует точка с Î (a, b), в которой функция y = f (x) принимает наибольшее или наименьшее значение, и по теореме Ферма f ¢ (с) = 0.

Доказательство закончено.

Геометрически теорема Ролля означает, что у графика непрерывной на отрезке и дифференцируемой внутри него функции, принимающей на его концах одинаковые значения, существует точка, в которой касательная параллельна оси Ох (см. рис. 18.18).

Из теоремы Ролля вытекает еще один важный вывод.

Напомним, что нулем функции y = f (x) называется точка с такая, что f (с) = 0. Пусть функция y = f (x) удовлетворяет условиям теоремы Ролля, тогда между двумя нулями функции y = f (x) всегда лежит хотя бы один нуль ее производной: f ¢ (с) = 0, с Î (x₁ , x₂) (см. рис. 18.19).

Теорема 18.5 (Теорема Лагранжа о конечном приращении). Пусть функция y = f (x):
1) непрерывна на отрезке [ a, b ];
2) дифференцируема в каждой точке интервала (a, b);
Тогда существует хотя бы одна такая точка с Î (a, b), что

или f (b) – f (а) = f¢ (с) (b - a) (18.33)

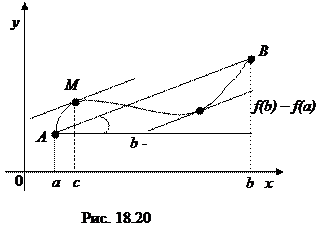Доказательство. Рассмотрим вспомогательную функцию F (x) = f (x) - l(x), которая непрерывна на отрезке [ a, b ] и дифференцируема в интервале (a, b) при любом выборе числа l, причем F¢ (x) = f¢ (x) - l. Выберем l так, чтобы F (а) = F (b), т. е. чтобы f (а) - l a = f (b) - l b. Отсюда получим . Тогда для функции F (x) выполняются все условия теоремы Ролля. Поэтому существует хотя бы одна точка с Î (a, b) такая, что F¢ (с) = 0, т. е. f ¢ (с) - l= 0 и f ¢ (с) = l. Окончательно получаем

Геометрический смысл теоремы Лагранжа состоит в следующем. Пусть
А (а, f (а)), В (b, f (b)) – концы графика функции y = f (x), АВ – хорда, соединяющая точки А и В (см. рис 18.20). Отношение есть угловой коэффициент хорды АВ, т. е. тангенс угла наклона хорды к оси Ох, а производная f¢ (с) – угловой коэффициент касательной к графику функции y = f(x) в точке

М(с, f (с)).

Таким образом, теорема Лагранжа показывает, что в интервале (a, b) существует точка с, в которой касательная к графику параллельна хорде АВ.

Следствие 1. Если функция y = f(x) непрерывна на отрезке [a, b] и в интервале (a, b) имеет производную, равную нулю, f¢ (с) = 0 "x Î (a, b), то функция постоянна на отрезке
[a, b]: f(x) = с = const.

Доказательство. Выберем произвольно точки x1, x2 Î [a, b], x1 < x2. Тогда на отрезке
[x1, x2] Ì [a, b] функция y = f(x) удовлетворяет условиям теоремы Лагранжа, поэтому существует точка с Î (x1, x2) такая, что f (x2) – f (x1) = f¢ (с) (x2 - x1). По условию, f¢ (х) = 0 на (а,b), в частности f¢ (с) = 0. Поэтому f (x2) – f (x1) = 0 и f (x2) = f (x1) для любых x1, x2 Î [a, b]. Это и означает, что функция y = f(x) постоянна на отрезке [a, b].

Следствие 2. Пусть функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы в интервале (a, b). Если они имеют равные производные f¢ (x) = g¢ (x) для всех х Î (a, b), то эти функции отличаются лишь на константу:

f(x) = g(x) + С, (18.34)

где С – константа.

Доказательство. Функция F(x) = f(x) - g(x) удовлетворяет условиям следствия 1 и F¢ (x) =
= f¢ (x) - g¢ (x) = 0 "х Î (a, b). Поэтому F(x) = С = const, т. е. f(с) - g(с) = С.

Замечание. Рассмотрим приращение Dу = f(x) - f(x0) функции f(x) в точке x0. По теореме Лагранжа существует такая точка с, лежащая между точками x0 и x, что f(x) - f(x0) = f¢ (с) (x- x0) или Dу = f¢ (с) Dх.
В таком виде теорему Лагранжа называют теоремой о среднем или формулой конечных приращений.

Теорема 18.6. (Теорема Коши). Пусть функции f (x) и g (x):
1) непрерывны на отрезке [ a, b ];
2) дифференцируема в каждой точке интервала (a, b);
3) g¢ (x) ¹ 0 в каждой точке интервала (a, b).
Тогда существует точка с Î (a, b) такая, что

(18.35)

Доказательство этой теоремы аналогично доказательству теоремы Лагранжа: вводим вспомогательную функцию F (x) = f (x) - l g (x), где l выбрано из условия F (а) = F (b), формула (18.35) вытекает теперь из теоремы Ролля (предлагаем читателю восстановить детали доказательства самостоятельно).

Дата добавления: 2015-07-20