Производные и дифференциалы высших порядков.

Пусть функция y=f (x) дифференцируема в окрестности точки x ₀. Тогда ее производная y¢=f¢ (x)сама является функцией переменной х в указанной окрестности точки х ₀ и может иметь производную в этой точке, называемую производной второго порядка или второй производной функции y=f (x) в точке х ₀, которую обозначают одним из символов

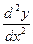, у¢¢, , f¢¢ (x ₀), (читаем 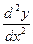– “дэ два игрек по дэ икс дважды”, у¢¢ – “игрек два штриха”). Итак,

f¢¢ (x ₀)= = ,

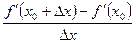если этот предел существует.

Производную y¢=f¢ (x) называют первой производной функции y=f (x). Тогда можно сказать, что вторая производная – это производная от первой производной.

Аналогично определяется производная третьего порядка у¢¢¢= (у¢¢) ¢, т.е. как производная от второй производной. Производная n -го порядка у ^{( n )}есть производная от (n -1)-й производной:

у ^{( n )}=[ у ^{( n -1)}]¢.

Таким образом, что бы найти производную n -го порядка, необходимо найти все производные у¢, у¢¢, у¢¢¢, у ⁽⁴⁾, …, у ^{( n -1)} до n -1 включительно.

Обозначение n -й производной: у ^{( n )}, f ^{( n )}, , .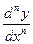

Производные порядка выше третьего обозначаются числом в скобках: у ⁽⁴⁾ – производная четвертого порядка.

Производные порядков выше первого называются производными высших порядков.

При вычислении высших производных используются все ранее изученные правила дифференцирования.

Приведем лишь формулу Лейбница, обобщающую правило нахождения производной произведения двух функций.

Пусть y=uv, где u=u (x) и v=v (x) имеют производные до порядка n включительно. Тогда справедлива формула Лейбница:

у ⁽ⁿ⁾=(uv)⁽ⁿ⁾= = u ⁽ⁿ⁾ v+n u ^{(n- 1)} v¢ + u ^{(n -2)} v¢¢¢ +…+ u v ⁽ⁿ⁾. (18.24)

В частности,

y¢¢= (uv)¢¢= u¢¢v+ 2 u¢v¢+uv¢¢,

y¢¢¢=u¢¢¢v+ 3 u¢¢v¢+ 3 u¢v¢¢+uv¢¢¢.

Пример 18.16. Вычислим n -производную функции y = sin x. Используя формулу приведения sin (x+p /2) = cos x, получим последовательно:

y¢ =cos x = sin (x+p /2), y¢¢= cos (x+p /2) = sin (x+ p /2+ p /2) = sin (x+2 p /2),

y¢¢¢ = cos (x+2 p /2) = sin (x+3 p /2),..., у ^(k) = sin (x+k p /2),....

Итак,

(sin x)⁽ⁿ⁾ = sin (x+ ).

Аналогично,

(cos x)^{( n )} = cos (x+ ).

Пример 18.17. Пусть y = x² e^3x. Найдем y ⁽¹⁰⁾.

Решение. Положим v = х² и u = е^3х. Тогда находим

v¢= 2х, v¢¢ = 2, а v ^{( k )} = 0 при k ³ 3.

Далее, u¢ = 3 e^3x, u¢¢ = 3² e^3x,..., u ^{( k )} = 3 ^ke^3x, в частности,

u ⁽⁸⁾ = 3 ⁸e^3x, u ⁽⁹⁾ = 3 ⁹e^3x, u ⁽¹⁰⁾ = 3 ¹⁰e^3x.

По формуле Лейбница получим

у ⁽¹⁰⁾=(uv)⁽¹⁰⁾= = = 3¹⁰ х ² e^3x + 10 3⁹ e^3x 2 x +

+ 45 3⁸ e^3x 2 = 3⁸ (9 x² + 60 x + 90) e^3x = 3⁹ (3 x² +20 x + 30) e^3x.

Перейдем к определению дифференциалов высших порядков. Пусть функция y=f (x) дифференцируема в некотором интервале (a,b). Тогда ее дифференциал d y = f¢ (х)d х являетсяфункцией, зависящей как от независимой переменной х, так и от ее дифференциала d х. Заметим, что d х есть произвольное и независящее от х число, которое при дифференцировании по х рассматривается как постоянный множитель, ведь при заданном значении аргумента х значения дифференциала (приращения) d х= Dх могут выбираться произвольно.

Заметим еще, что дифференциал функции еще называется ее первымдифференциалом.

Таким образам, дифференциал функции d y = f¢ (х)d х, являясьфункцией переменной х, сам может иметь дифференциал, называемый дифференциаломвторогопорядка или вторымдифференциалом функции y=f (x) и обозначается d² y (читаем: “дэ два игрек”):

d² y = d(d y),

т. е. второй дифференциал – это дифференциал от первого дифференциала. Аналогично определяются дифференциалы более высоких порядков. В частности, дифференциалом п -гопорядка d ^пy называется дифференциал от дифференциала (п- 1)-го порядка как функции переменной х:

d(d ^{п -1} y).

Учитывая все выше сказанное, получим

d² y = d(d y) = (d y)¢ d х = (f¢ (х) d х)¢ d х = f¢¢ (х) d х²,

где d х² = (d х)² (не путать с дифференциалом функции у = х ²: d y = (d х²) = 2 х d х).

Аналогично имеем для дифференциала п- го порядка

	d ^пy = у^(п) d x

или (18.25)

Из последней формулы следует, что

у ^(п) = .

Дата добавления: 2015-07-20