Параметрическое задание функции и ее дифференцирование.

Пусть даны две функции x = j(t), y = y(t) одной независимой переменной t, определенные и непрерывные в некотором интервале (a, b). Если функция x = j(t) строго монотонна, то она имеет обратную функцию t = F(x), непрерывную и монотонную в некотором интервале (a, b). Поэтому y является сложной функцией, зависящей от переменной x посредством переменной t, называемой параметром:

y = f (x) = y(F(x)), x Î (a, b).

Эта функция непрерывна по теореме о непрерывности сложной функции. Итак, система функций (18.26)
определяет функцию y = f (x) переменной x, а сами уравнения (18.26) называются параметрическими уравнениями функции y = f (x) (см. рис. 18.13). Такой способ задания функции называется параметрическим. Пример 18.18. Рассмотрим функцию y = f (x), заданную параметрически системой уравнений (а > 0)

t Î [ 0,p] (18.27)

Так как функция 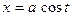убывает на отрезке [ 0,p] (см. рис. 18.14), то существует обратная функция t = F(x) = arccos , x Î[ -a,a ]. Если подставим ее во второе уравнение вместо t, то получим искомую функцию в явном виде: y = a sin(arccos ) =
= a . Знак плюс перед корнем выбираем в силу того, что функция y = a sin t неотрицательна при t Î [ 0,p]. Таким образом, уравнения (18.27) есть параметрические уравнения функции y = , x Î [ -a,a ], графиком которой является верхняя полуокружность (см. рис. 18.15). Взяв p £ t £ 2p, получим, что система (18.27) есть параметрические уравнения функции y = f (x) = – , графиком которой является нижняя полуокружность (см. рис. 18.15).

Пусть функции x = j(t) и y = y(t) дифференцируемы в области определения (a, b) и y¢(t) ¹ 0.
Тогда обратная функция t = F(x) дифференцируема и 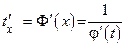. По теореме о
производной сложной функции получим

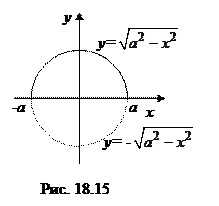
. Следовательно,

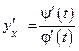или, короче, . (18.28)

Таким образом, производная функции, заданной параметрически, сама является функцией, заданной параметрически:

если t Î (a, b), то з t Î (a, b).

Найдем вторую производную функции, заданной параметрически уравнениями (18.26). Так как вторая производная есть производная от первой производной, то, согласно формуле (18.28), получим

. (18.29)

Аналогично можно получить производную от у по х любого порядка.

Дата добавления: 2015-07-20