Правило Лопиталя раскрытия неопределенностей.

В параграфе 16 мы рассмотрели понятие неопределенности, некоторые виды неопределенностей и способы их раскрытия. Сейчас рассмотрим простой и эффективный метод раскрытия неопределенностей: правило Лопиталя.

Теорема 18.7. (Правило Лопиталя раскрытия неопределенности вида ).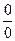

Пусть функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки а, за исключением, быть может, самой точки а. Если

1) = 0, т.е. f (x) и g (x) – б. м. при х ® а;

2) g¢ (x) ¹ 0 в указанной окрестности точки а;

3) существует предел , конечный или бесконечный,

то существует предел 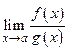и справедливо равенство

(18.36)

Теорема 18.8. (Правило Лопиталя раскрытия неопределенности вида ).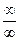

Если в условиях теоремы 18.7 первое условие заменить на условие = , т.е. f (x) и g (x) – б. б. функции при х ® а, то формула (18.36) остается в силе.

Заметим, что эти теоремы справедливы и для случаев, когда х ® а- 0 или х ® а+ 0.

Неопределенности вида 0 ¥ и ¥ - ¥ необходимо свести к неопределенностям вида 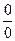и 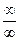и раскрыть по правилу Лопиталя.

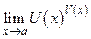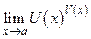Неопределенности вида 0⁰, 1^¥, ¥⁰ возникают при вычислении пределов вида . С помощью логарифмирования сводим эти типы неопределенности к неопределенности вида 0 ¥. Действительно, если = А, то ln A = =
= (0 ¥) = k, тогда 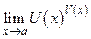= А = e ^{ln A} = e ^k.

Пример 18.21. Найти пределы 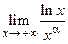и .

Решение.

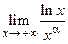= = 0,

= (0 ¥) = = 0.

Пример 18.22. Найти предел .

Так как , , то мы имеем неопределенность 1^¥. Далее положим = А и, логарифмируя, находим k = ln A = = ==

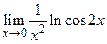окончательно получим = (1^¥) = А = e ^{ln A} = e ^k = e ^–2 = .

Дата добавления: 2015-07-20