Формула Маклорена некоторых элементарных функций.

1. y=f (x)= е^х.

Так как у ^(к)= е^х, у ^(к)(0)=1, для всех к = 0, 1, 2, …, n, то справедлива формула Маклорена

е^х= (хⁿ)=1+ (хⁿ). (18.49)

2. y=f (x)=sin x

Так как у ^(к)=sin , у ^(к)(0)=sin , то формула Маклорена имеет вид

(х ^{2 n +2})= х- 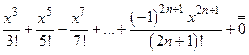(х ^{2 n +2}). (18.50)

Нечетность функции y =sin x нашла отражение и в формуле Маклорена: многочлен Тейлора имеет только нечетные степени х.

3. y =cos x.

cos x = (х ^{2 n +1})=1- (х ^{2 n +1}). (18.51)

4. у= ln (1+ х).

у¢= = (1+ х)^-1, у¢¢= (-1)(1+ х)^-2, у¢¢¢= (-1)(-2)(1- х)^-3, у ^(к)=(-1) ^{к- 1}•(к -1)! (1- х)^{- к} , отсюда

у ^(к)(0)= f ^{( k )}(0)= (-1) ^{к- 1}•(к -1)! Тогда ln (1+ x)= (хⁿ)=

= х - (х ⁿ). (18.52)

5. y= (1+ x) ^α, α Î R.

Так как у^к=α (α- 1)…(α–к +1)(1+ х) ^α-к и у^к (0) =α (α- 1)…(α–к +1), тогда

(1+ х) ^α =1+ =

=1+ αх+ . (18.53)

Дата добавления: 2015-07-20