
Читайте также:
|
Пусть функция y=f (x) определена в некоторой окрестности точки х 0 и имеет в точке х 0 производные до порядка n включительно.
Многочлен
Tn (x)=  (х-х 0) к = f (х 0)+
(х-х 0) к = f (х 0)+  (18.41)
(18.41)
называется многочленом Тейлора степени n функции y=f (x) в точке х 0.
Многочлен Тейлора (18.41) функции y=f (x) обладает тем свойством, что его производные в точке х 0 совпадают с соответствующими производными функциями y=f (x) в точке х 0:
 = f ( k )(x 0), к = 0, 1, …, n.
= f ( k )(x 0), к = 0, 1, …, n.
Для этого нужно вычислить многочлен Тn (x) и его производные в точке х 0.
Представление
f (x)= Tn (x)+ Rn (x)=  (х-х 0) к + Rn (x) (18.42)
(х-х 0) к + Rn (x) (18.42)
называется формулой Тейлора функции y=f (x) в точке х 0, где Rn (x)= f (x)- Тn (x) называется остаточным членом формулы Тейлора.
Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию y=f (x) в виде многочлена (многочлена Тейлора Tn (x)) и дать оценку погрешности этого приближения (оценив остаточный член формулы Тейлора Rn (x)).
Теорема 18.9. (Формула Тейлора с остаточным членом в форме Пеано). Пусть y=f (x) имеет в точке х 0 производные до порядка n включительно. Тогда при х → x 0
Rn (x)=  ((х-х 0) n) и f (x)=
((х-х 0) n) и f (x)=  (х-х 0) к +
(х-х 0) к +  ((х-х 0) n). (18.43)
((х-х 0) n). (18.43)
Это и есть формула Тейлора функции y=f (x) с остаточным членом в форме Пеано.
Теорема 18.10. (формула Тейлора с остаточным членом в форме Лагранжа). Пусть функция y=f (x) определена в некоторой окрестности точки х 0 и имеет в этой окрестности производные до (n +1)-го порядка включительно. Тогда для любого х из этой окрестности найдется точка с Î(х 0, х) такая, что
Rn (x)=  (х-х 0) n+ 1 и f (x)=
(х-х 0) n+ 1 и f (x)=  (х-х 0) к +
(х-х 0) к +  (х-х 0) n+ 1. (18.44)
(х-х 0) n+ 1. (18.44)
Это и есть формула Тейлора функции y=f (x) с остаточным членом в форме Лагранжа.
Замечание 1. Остаточный член формулы Тейлора в форме Лагранжа позволяет оценивать степень приближения функции y=f (x) ее многочленом Тейлора Tn (x). Пусть (n +1)-я производная f ( n +1)(x) ограничена в окрестности точки х 0, т.е. существует число М >0 такое, что | f ( n +1)(x)|≤ М для всех х из указанной окрестности. Тогда справедливо неравенство
| Rn (x)|≤ 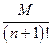 •| x-x 0| n+ 1. (18.45)
•| x-x 0| n+ 1. (18.45)
Замечание 2. Формула Тейлора в форме дифференциалов.
Заметим, что f (к)(x 0) (х-х 0) к = f (к)(x 0) D хк= f (к)(x 0) dxk=dk f (x 0), а х-х 0=D х, то формулу (18.43) можно записать в виде
f (x)=  dk f (x 0)+
dk f (x 0)+  ((D х) n)= f (x 0)+
((D х) n)= f (x 0)+  df (x 0)+
df (x 0)+ 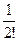 d 2 f (x 0)+…+
d 2 f (x 0)+…+ 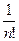 dn f (x 0)+
dn f (x 0)+  ((D х) n), (18.46)
((D х) n), (18.46)
Замечание 3. Формула Тейлора функции y=f (x) в точке х 0=0 называется формулой Маклорена.
Формула Маклорена с остаточным членом в форме Пеано:
f (x)= 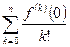 хк +
хк +  (хn)= f (x 0)+
(хn)= f (x 0)+  x +
x + 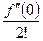 x 2+…+
x 2+…+  xn +
xn +  (хn). (18.47)
(хn). (18.47)
Формула Маклорена с остаточным членом в форме Лагранжа:
f (x)= 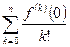 хк +
хк +  хn+ 1= f (0)+
хn+ 1= f (0)+  x +
x + 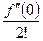 x 2+…+
x 2+…+  xn +
xn +  хn+ 1 (18.48)
хn+ 1 (18.48)
Дата добавления: 2015-07-20; просмотров: 124 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формула Тейлора для многочлена. | | | Формула Маклорена некоторых элементарных функций. |