Выпуклость вогнутость. Точки перегиба.

Пусть функция дифференцируема в интервале , т.е. график функции имеет касательную в каждой своей точке.

Функция называется выпуклой в интервале , если ее график расположен под любой ее касательной в этом интервале (см. рис. 19.9.).

Функция называется вогнутой в интервале , если ее график расположен над любой ее касательной в этом интервале (см. рис. 19.9.).

Рис. 19.9. Рис. 19.10.

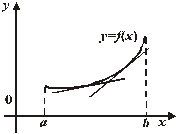Интервалы выпуклости вогнутости графика функции находим с помощью второй производной функции.

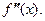Теорема 19.5. Пусть функция имеет в интервале вторую производную Тогда

1) если 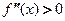в интервале , то функция вогнута в этом интервале;

2) если 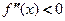в интервале , то функция выгнута в этом интервале.

Геометрически теорема ясна (см. рис. 19.11). Если 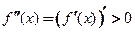, то функция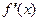 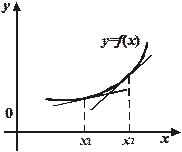возрастает в интервале , т.е. возрастает угол наклона касательных к графику, что и означает вогнутость функции в этом интервале.

Аналогично рассматривая случай 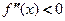в (см. рис. 19.9).

Особый интерес представляют точки, в которых меняется характер выпуклости функции.

Точкой перегиба графика дифференцируемой функции называется точка, разделяющая интервалы выпуклости и интервалы вогнутости функции.

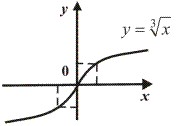
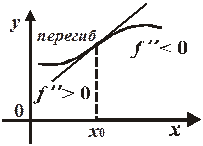
В точке перегиба график функции переходит с одной стороны касательной, проведенной в точке перегиба на другую (см. рис. 19.12 и 19.13).

Рис. 19.12. Рис. 19.13.

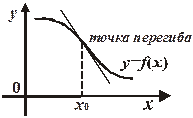Из вышесказанного следует, что точки перегиба – это точки экстремума первой производной. Отсюда вытекают следующие утверждения.

Теорема 19.6. (необходимое условие точки перегиба).

Пусть - точка перегиба графика дифференцируемой функции . Если в точке существует вторая производная функции, то обязательно .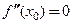

Вывод: Возможные точки перегиба графика дифференцируемой функции следует искать среди ее критических точек высокого рода, т.е. среди точек, в которых вторая производная функции либо равна нулю, либо не существует.

Теорема 19.7. (достаточное условие точки перегиба).

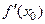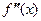Пусть функция дважды дифференцируема в некоторой окрестности точки , за исключением, быть может, самой точки , и имеет в точке первую производную . Если при переходе через точку вторая производная меняет знак, то - точка перегиба (см. рис. 19.14).

Рис. 19.14.

Изобразим это в виде схемы:

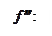
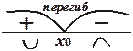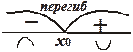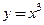Пример 19.1. Исследуем поведение функции и 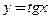в окрестности точки 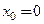и постоим их графики в окрестности этой точки.

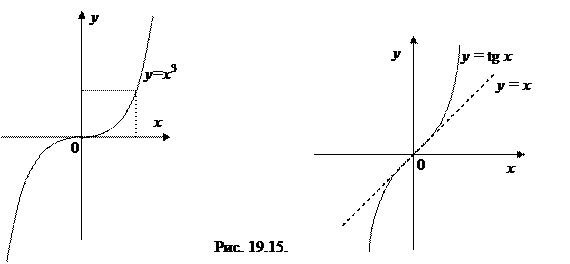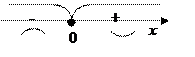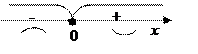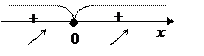
у=х ^2 1) у = х^3 у¢= 3х^2, у¢(0) = 0, у¢: у¢¢= 6х, у¢¢(0) = 0, у¢¢: Итак: х0 = 0 – точка перегиба, у = 0 – уравнение касательной в точке перегиба

2) у = tg x y¢ = 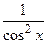= tg^2 x +1, y¢(0) = 1,   y¢:   y¢¢ = 2 tg x 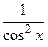, у¢¢(0) = 0   Итак: х0 = 0 – точка перегиба, у = х – уравнение касательной в точке перегиба

Этот пример показывает значение касательной в точке перегиба. При исследовании их поведения в точке х = 0 бросается в глаза внешнее сходство свойств этих функций в окрестности нуля. И только касательная, проведенная в точке перегиба, показывает все различие в поведении этих функций в окрестности нуля.

Дата добавления: 2015-07-20