Решение.

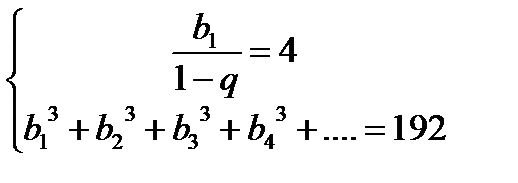
Из первого уравнения получаем .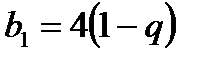

Из второго уравнения ;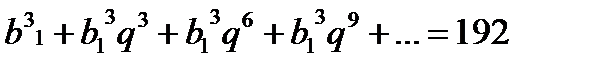

;

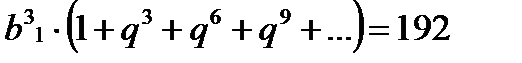Выражение в скобках представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем и 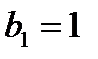, поэтому его можно заменить на .

Подставив 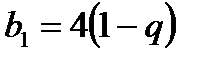, получаем ; .

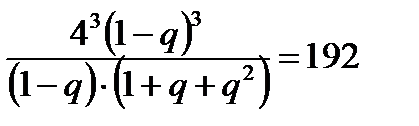Преобразовывая, получаем 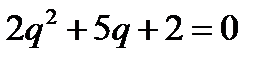, откуда .

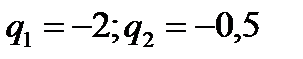Так как прогрессия убывающая выбираем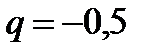

Находим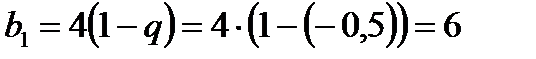

Ответ: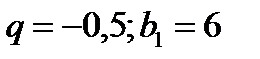

Задача 7. После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда после шести движений поршня, если первоначально давление было 760 мм. рт. ст.

Решение: Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление предыдущего движения поршня умножить на 0,8.

Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм. рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Таким образом, . Применяем формулу

Ответ: 199,23 мм рт.ст.

Дата добавления: 2015-10-21