
Читайте также:
|
1. Выразить  через
через 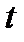 , где
, где  и вычислить значение выражения
и вычислить значение выражения  при
при 
Решение. 
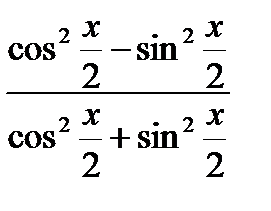 .
.
Поделим числитель и знаменатель дроби на выражение  ,
,
получаем  .
.
Аналогично получаем остальные формулы:
 ,
, 

 ;
;
преобразуем 
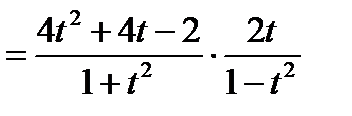 ;
;
далее 
Ответ: 
2. Упростить: 
 .
.
Решение. Для упрощения этого выражения применяем формулу синуса двойного аргумента и основное тригонометрическое тождество.


Ответ: 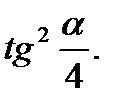
3. Решить уравнение 
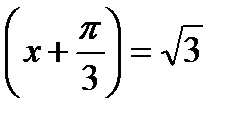 .
.
Решение. 



 ;
; 



 ;
;  ,
,  .
.
Ответ:  ,
,  .
.
4. Найти корни уравнения 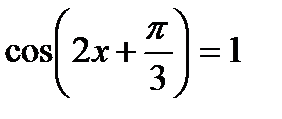 на интервале
на интервале 
Решение. 
Используем типовую формулу:  ,
,  .
.
Та как  , то
, то  , поскольку для нахождения корней задан промежуток [0;π]. Тогда
, поскольку для нахождения корней задан промежуток [0;π]. Тогда  .
.
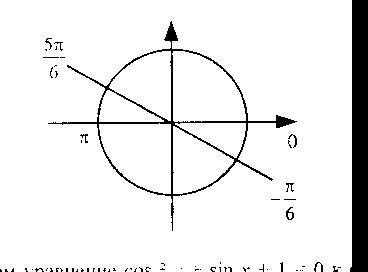
Поскольку это значение корня не входит в заданный в условии промежуток, возьмем симметричное ему значение (т.к. функция косинус симметрична относительно оси ординат) – это  , это значение входит в заданный промежуток и является решением уравнения.
, это значение входит в заданный промежуток и является решением уравнения.
Ответ: 
5. Решить уравнение 

. Решение. Воспользуемся формулой разности косинусов двух углов:

 ,
,
 ,
,
 ,
,
 ,
,
 ,
,

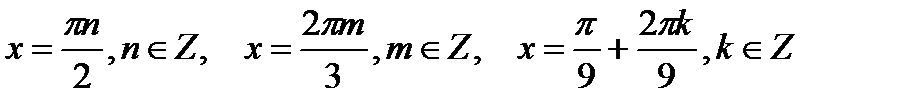
Ответ: 
6. Решить уравнение 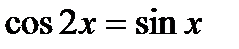 на интервале (0; 180о).
на интервале (0; 180о).
Решение: Для решения уравнения 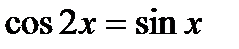 применим формулу двойного аргумента для косинуса:
применим формулу двойного аргумента для косинуса:  .
.
Чтобы привести уравнение к однородному виду, заменим соs2 x на 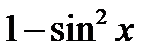 , получаем
, получаем 
 , сделаем замену:
, сделаем замену: 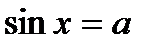


Вернемся к замене: 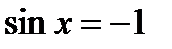 – это значение синуса не входит в заданный в условии интервал (0; 180о)
– это значение синуса не входит в заданный в условии интервал (0; 180о)
 табличное значение,
табличное значение,  и
и  , поскольку на интервале (0; 180о) оба эти угла соответствуют одному и тому же значению синуса.
, поскольку на интервале (0; 180о) оба эти угла соответствуют одному и тому же значению синуса.

Ответ:  и
и  .
.
7. Решить уравнение: 
Решение. Преобразуем левую часть уравнения по свойству степеней


Обозначим  получим:
получим:
 или
или 
Вычисляем дискриминант и корни квадратного уравнения:
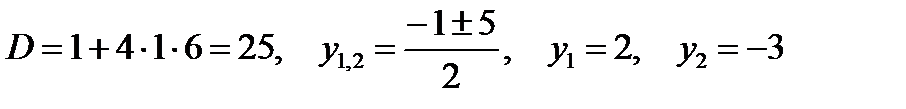 (не удовлетворяет).
(не удовлетворяет).
 так как
так как  то
то 
Воспользуемся формулой: 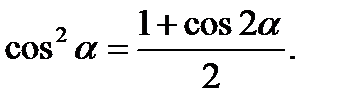
Тогда уравнение примет вид:
 ,
,
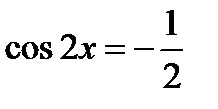 ,
,
 ,
,
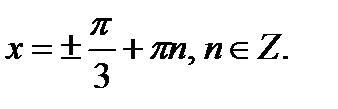
Ответ: 
8. Решить уравнение:
 .
.
Решение. Преобразуем исходное уравнение, используя известные тригонометрические формулы.

Раскроем скобки и приведем подобные слагаемые в этом уравнении.
 ;
;
 ;
;
 .
.
Пусть  , где
, где  .
.
Тогда, после замены переменной, уравнение примет вид:  .
.
Решая это квадратное уравнение, получим:  и
и  . Второй корень является посторонним, так как он не удовлетворяет условию
. Второй корень является посторонним, так как он не удовлетворяет условию 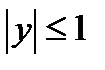 .
.
Итак, получим:  ;
; 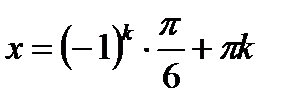 , где
, где  .
.
Ответ: 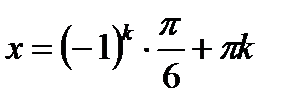 , где
, где  .
.
9. Решить уравнение: 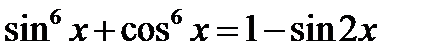 .
.
Решение. Для решения этого уравнения используем основное тригонометрическое тождество: 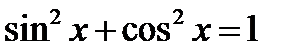 .
.
Возведем в третью степень обе части этого тождества:
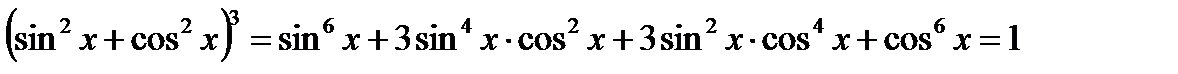 .
.
Поэтому левую часть исходного уравнения можно записать в виде:
 .
.
Тогда уравнение примет вид:
 ;
;
 ;
;
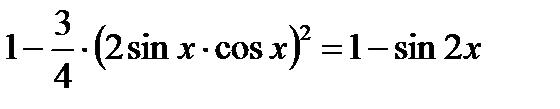 .
.
Используя формулу для синуса двойного угла, получим:
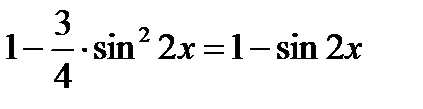 ;
;
Приведем подобные слагаемые и сделаем замену переменной  , где
, где 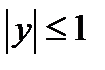 . Тогда получим квадратное уравнение
. Тогда получим квадратное уравнение  , которое имеет корни:
, которое имеет корни:
 и
и  . Второй корень является посторонним, так как он не удовлетворяет условию
. Второй корень является посторонним, так как он не удовлетворяет условию  .
.
Итак, получим:  , поэтому
, поэтому 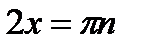 , где
, где  .
.
Окончательно имеем:  , где
, где 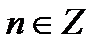 .
.
Ответ:  .
.
10. Решить неравенство  .
.
Решение.
| t 1 |
| – |
| l |
| t 2 |
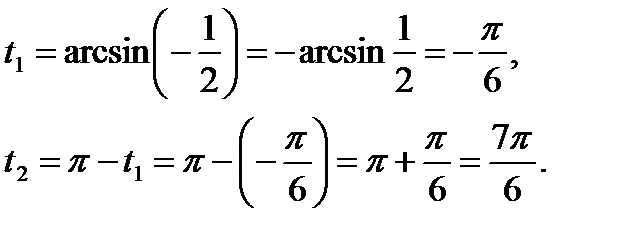
С учетом периода синуса, запишем ответ:
 .
.
Ответ: 
Дата добавления: 2015-10-21; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Целесообразно решать тригонометрические неравенства методом интервалов. | | | Задачи для работы в аудитории |