Методы решения показательных уравнений.

Уравнивание оснований степеней.

Пример. Решить уравнение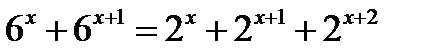

Решение: Выносим общий множитель в правой и левой части уравнения

или .

Преобразовываем к виду 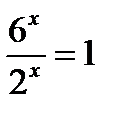; ; 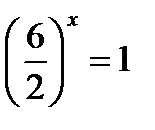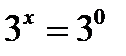, откуда получаем .

Ответ: 0

2) Решение с помощью логарифмирования.

Пример. Решить уравнение

Решение: Логарифмируя обе части уравнения с помощью натурального логарифма и применяя правило логарифмирования степени, получаем

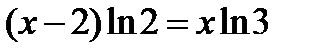; ; , откуда .

Ответ: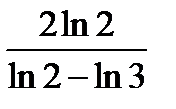

3) Введение вспомогательной переменной.

Пример. Решить уравнение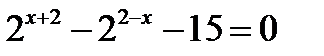

Решение: Представим в виде .

Сделаем замену , где , в результате получаем

; .

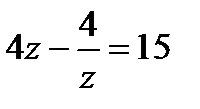Решая полученное квадратное уравнение находим корни

и (не принадлежит ОДЗ). Таким образом, получаем 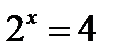или 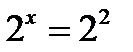, откуда .

Ответ: 2

Методы решения логарифмических уравнений.

Дата добавления: 2015-10-21