Отражение

1. Построение графика функции вида y=f(-x); f(x) f(-x)

Для построения графика функции y=f(-x) следует построить график функции y=f(x) и отразить его относительно оси ординат.

Пример 3. Построить график функции .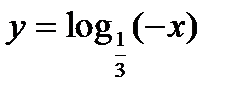

Решение. Строим график функции (рис. 11 –пунктирная линия) и отражением его относительно оси ординат получаем график функции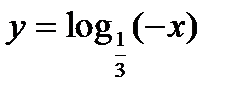

Пример 4. Построить график функции y=arcos(-x).

Решение. Строим график функции y=arccos(x) (рис. 12 –пунктирная линия) и отражением его относительно оси ординат получаем график функции y=arcos(-x).

Рис. 11 Рис. 12

2. Построение графика функции вида ;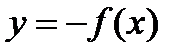

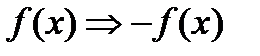
Для построения графика функции 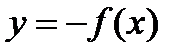следует построить график функции y=f(x) и отразить его относительно оси абсцисс.

Пример 5. Построить график функции .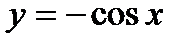

Решение. Строим график функции y=cos(x). (рис.13 – пунктирная линия) и отражением его относительно оси абсцисс получаем график функции y=-cosx.

Пример 6. Построить график функции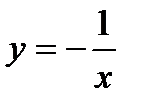

Решение. Строим график функции (рис.14 – пунктирная линия) и отражением его относительно оси абсцисс получаем график функции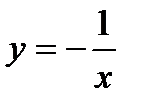

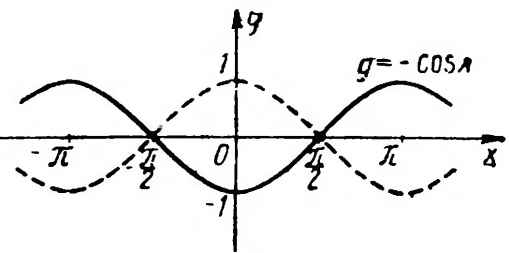
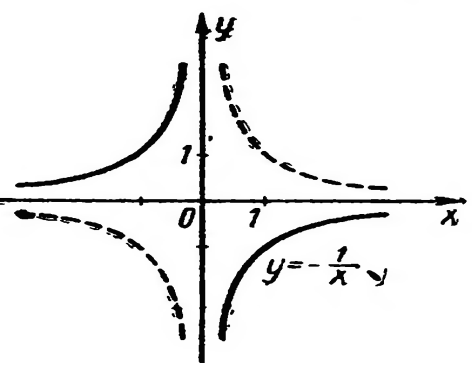
Рис.13 Рис. 14

3 Построение графиков четной и нечетной функций

Для построения графика четной функции y=f(x) следует построить ветвь графика этой функции только в области положительных значений аргумента х ≥ 0. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно оси ординат и получается отражением ее относительно этой оси.

Пример 7. Построить график функции .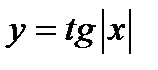

Решение. Исходная функция является четной, поэтому строим график функции в области положительных значений аргумента х ≥ 0, где она имеет вид y=tgx. Левую ветвь графика получаем отражением относительно оси ординат (рис. 15).

Пример 8. Построить график функции .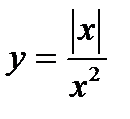

Решение. Данная функция – четная, поэтому достаточно построить ее график лишь в области положительных значений аргумента х > 0. График исходной функции в области отрицательных значений х получаем отражением относительно ординат (рис. 16).

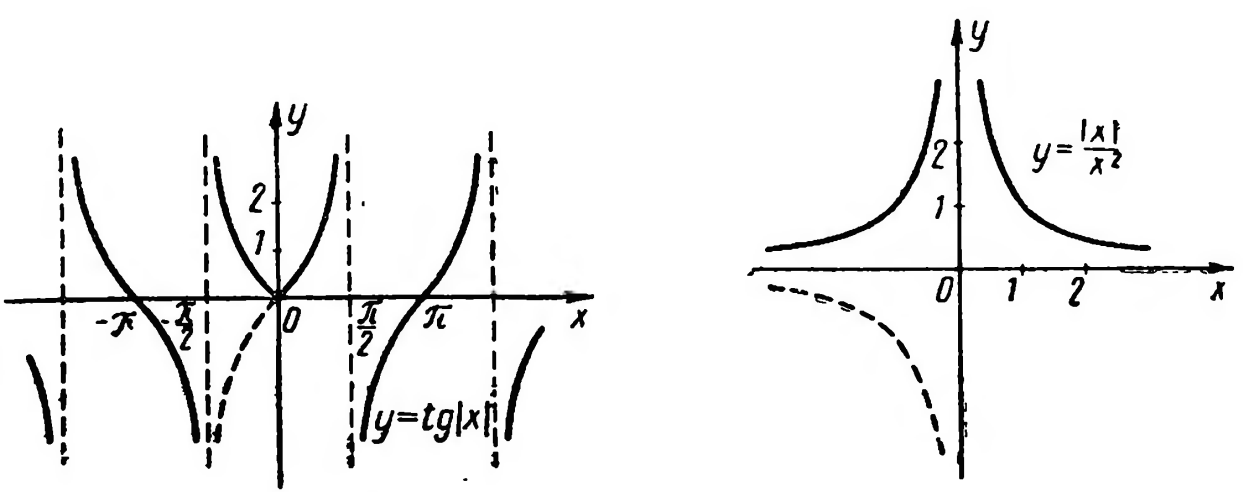
Рис. 15 Рис. 16

Для построения графика нечетной функции y=f(x) следует строить ветвь графика этой функции только в области положительных значений аргумента х ≥ 0. График функции y=f(x) в области отрицательных значений аргумента симметричен построенной ветви относительно начала координат и может быть получен отражением этой ветви относительно оси ординат с последующим отражением в области отрицательных значений х относительно оси абсцисс.

Пример 9. Построить график функции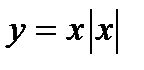

Решение. Исходная функция является нечетной, поэтому строим график функции в области положительных значений аргумента х ≥ 0, где она имеет вид .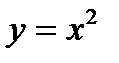

Левую ветвь графика получаем отражением построенной ветви относительно начало координат (рис. 17)

Пример 10. Построить график функции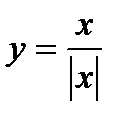

Решение. Данная функция является нечетной, поэтому строим ее график лишь в области х > 0 (точка х=0 не входит в область определения функции), где она имеет вид у=1. Левую ветвь графика получаем отражением построенной ветви относительно начало координат. На рисунке 18 стрелки означают, что точки х =0, у= 1 и х =0, у =-1 не принадлежать графику.

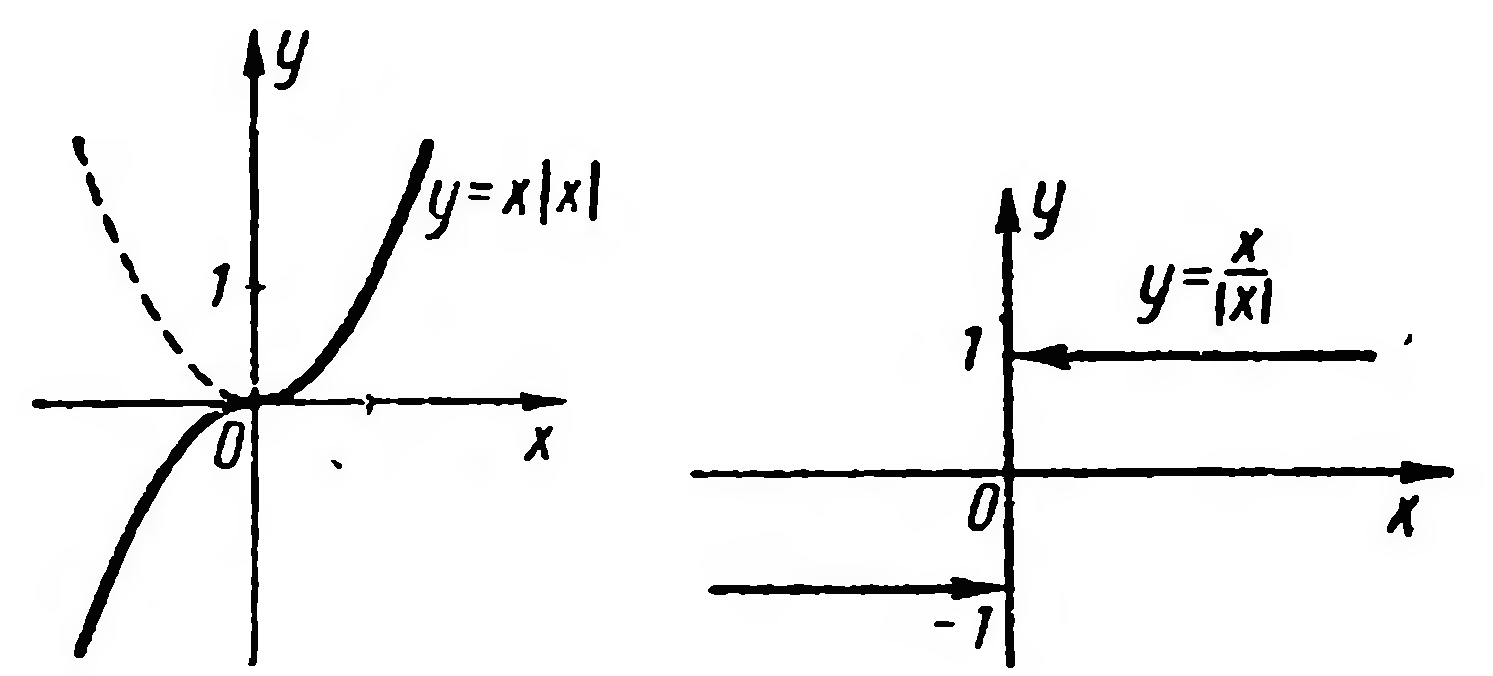
Рис. 17 Рис. 18

4. Построение графика обратной функции

Для построения графика функции 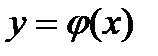, обратной по отношению к функции 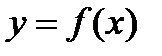, следует построить график 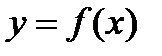и отразить его относительно прямой .

Пример 10. Построить график функции .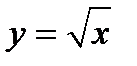

Решение. Рассмотрим график параболы у=х² (Рис. 19—пунктирная кривая) и график обратной к ней функции 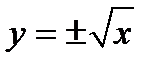, получаемой отражением параболы относительно прямой у=х.

Пример 11. Построить график функции .

Решение. Данная функция является обратной по отношению к функции у=х³, поэтому строим график функции у=х³ и отражением его относительно прямой у=х (рис. 20).

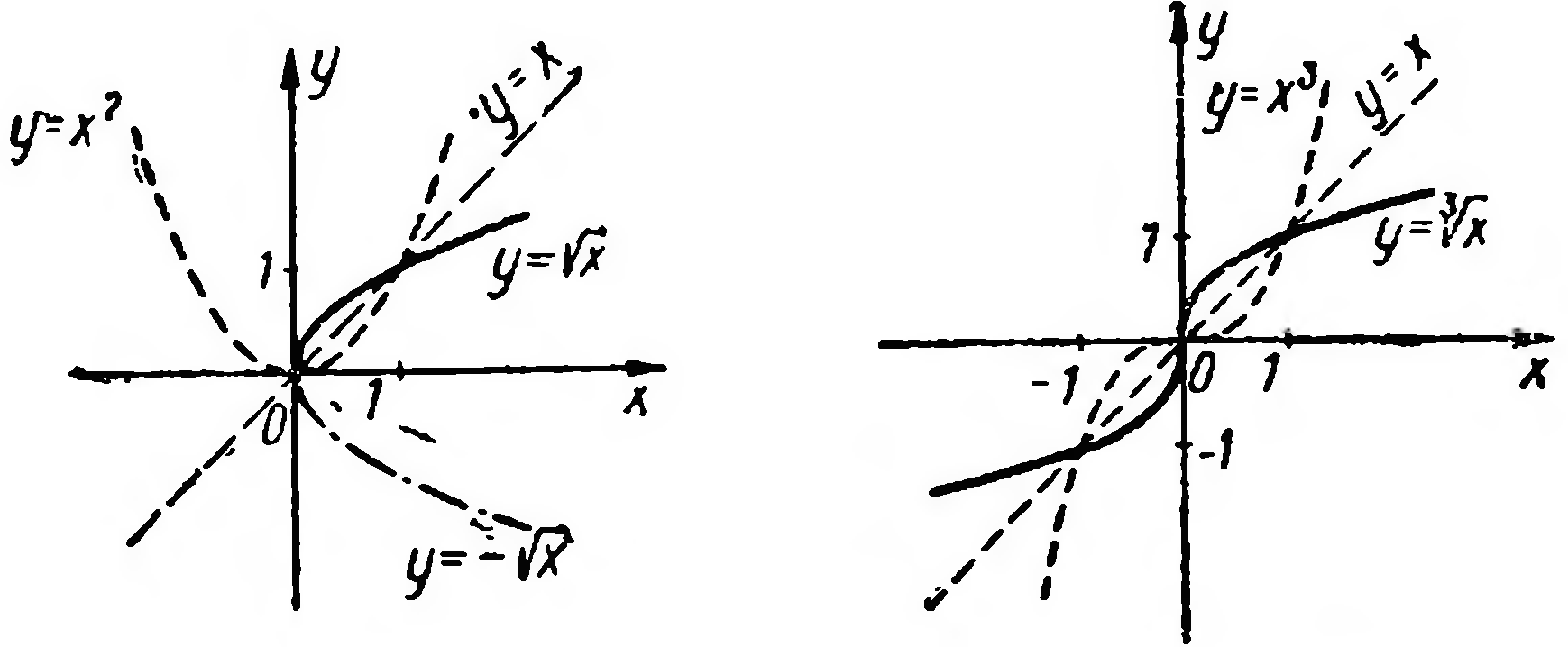
Рис. 19 Рис. 20

Дата добавления: 2015-10-21