Понятие функции

Введение

Необходимость написания данного методического пособия возникла в связи с введением новых стандартов специальностей и появление в учебных планах новой дисциплины «Математика 0» для студентов первого курса всех специальностей. На кафедре высшей математики была разработана рабочая программа по «Математике 0», содержание которой стало ориентиром при определении основных тем данного методического пособия. Пособие содержит теоретический материал, подробное решение типовых задач, задания для работы в аудитории с ответами, задания для самостоятельной работы с ответами для самопроверки, вопросы для самоконтроля и контрольные задания для аттестационной работы. Темы и задания по элементарной математике выбраны с учетом их дальнейшего использования при изучении курса высшей математики.

СОДЕРЖАНИЕ

	Функции действительной переменной. Определение. Примеры. Основные элементарные функции (степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические). Свойства. Графики ……………………………………………………………………………………..……..
	Преобразования графиков функций. Сдвиги графиков по осям координат. Симметрия графиков относительно осей координат, начала координат. Основные правила. Примеры использования..……...
	Многочлены. Определение. Теорема о разложении многочлена на множители. Деление многочлена на многочлен...……………………………………..…....……………… ……………………………………….
	Алгебраические уравнения и неравенства. Формулы сокращённого умножения. Разложение на множители. Метод интервалов……............................................................................…………...…………..
	Показательные и логарифмические уравнения и неравенства. Использование свойств показательной и логарифмической функций в решении задач………………………………………………………………..
	Основные соотношения в прямоугольном треугольнике. Тригонометрические уравнения и неравенства. Запись общего решения. Тригонометрические подстановки……………………………….
	Формулы площадей треугольника, параллелограмма, трапеции. Уравнения и неравенства с модулем. Графики функций, содержащих модуль………………………………………………………………….…
	Нахождение элементов арифметической и геометрической прогрессии: разности, знаменателя, сумм. Сумма бесконечно убывающей геометрической прогрессии…………………………..………………….
	Аннотация к дисциплине……………………………………………………………………………………..
	Вопросы для самоконтроля…………………………………………………………………………………..
	Список литературы……………………………………..…..………………………………………………….

ЗАНЯТИЕ 1.

ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ. ОПРЕДЕЛЕНИЕ. ПРИМЕРЫ. ОСНОВНЫЕ ЭЛЕМЕНТРАНЫЕ ФУНКЦИИ. СВОЙСТВА. ГРАФИКИ.

Понятие функции

Пусть даны два непустых множества Х и Y. Соответствие f. Которое каждому элементу x∈X сопоставляет один и только один элемент y∈Y, называется функцией и записывается y=f(x), x∈X или f:X→Y. Говорят ее, что функция f отображает множество Х на множество Y.

Рис.1

Например, соответствия f и g, изображенные на рисунке 1 а и б, являются функциями, а наа рисунке 1 в и г – нет. В случае в – не каждому элементу x∈X соответствует элемент y∈Y. В случае г не соблюдается условие однозначности.

Числовые функции. Способы задания функций. Графики функций.

Пусть задана функция .

Если элементами множеств X и Y являются действительные числа (т.е. и ), то функцию f называют числовой функцией.

Пусть задано числовое множество 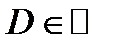. Если каждому числу 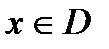поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция:

y = f (x), .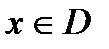

Множество D называется областью определения функции и обозначается D (f (x)). Множество, состоящее из всех элементов f (x), где 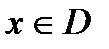называется областью значений функции и обозначается E (f (x)).

Число x часто называют аргументом функции или независимой переменной, а число y – зависимой переменной или, собственно, функцией переменной x.

Для того чтобы задать функцию f, нужно указать:

1) ее область определения D (f (x));

2) указать правило f, по которому каждому значению 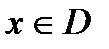ставится в соответствие некоторое значение y = f (x).

Область определения иногда еще называют областью допустимых значений функции (ОДЗ).

Пусть функции f (x) и g (x) определены на одном и том же множестве D. Тогда функция, значения которой в каждой точке 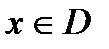равны f (x) + g (x), называется суммой функций f и g и обозначается f + g. Точно так же определяются разность f – g, произведение f · g и частное f / g двух функций (частное определено на множестве D, если на этом множестве g (x) ≠ 0).

Пусть функции y = g (x) и z = f (y) определены на множествах D и E соответственно, причем множество значений функции f содержится в области определения функции g. Тогда функция, принимающая при каждом 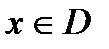значение f (g (x)), называется сложной функций или суперпозицией функций f и g и обозначается .

Дата добавления: 2015-10-21