Основные характеристики функций

1.Четность функции.

Функция f (x) называется четной, если для любого 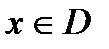выполняются условия:

а) ,
б) f (– x) = f (x).

График четной функции на всей области определения симметричен относительно оси OY. Примерами четных функций могут служить y = cos x, y = | x |, y = x ² + | x |.

Рис.2 График четной функции

Функция f (x) называется нечетной, если для любого 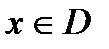выполняются равенства:
1) ,
2) f (– x) = – f (x).

Иными словами функция называется нечетной, если ее график на всей области определения симметричен относительно начала координат. Примерами нечетных функций являются y = sin x, y = x ³.

Если функция не четная и не нечетная, то это функция общего вида.

Исследование функций на четность облегчается следующими утверждениями.

· Сумма четных (нечетных) функций является четной (нечетной) функцией.

· Произведение двух четных или двух нечетных функций является четной функцией.

· Произведение четной и нечетной функции является нечетной функцией.

· Если функция f четна (нечетна), то и функция 1/ f четна (нечетна).

2. Монотонность функции

Пусть функция y=f(x) определена на множестве D и пусть 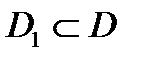. Если для любых значений 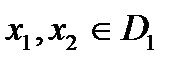аргументов из неравенства вытекает неравенство , то функция называется возрастающей на множестве ; , то функция называется неубывающей на множестве ; , то функция называется убывающей на множестве ; , то функция называется невозрастающей на множестве .

Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными.

3. Ограниченность функций

Функцию y=f(x), определенную на множестве D, называют ограниченной на этом множестве, если существует такое число М>0, что для всех выполняется неравенство . В противном случае функция является неограниченной.

Например, y = sin x и y = cos x – ограниченные функции, а и – неограниченные функции.

4.Периодичность функции

Функцию y=f(x), определенную на множестве D, называют периодической на этом множестве, если существует такое число Т>0, что при каждом значение и . При этом число Т называется периодом функции. Так, для y = sin x периодами будут числа

Дата добавления: 2015-10-21