Примеры решения задач. Решить уравнение

1. Решить уравнение .

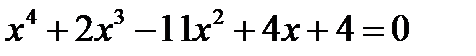Решение:

Чтобы проверить наличие целых корней этого уравнения, выпишем все делители его свободного члена: 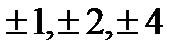. Подставляя по очереди эти числа в левую часть уравнения, находим, что числа 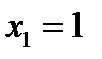и 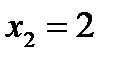являются корнями уравнения, т.е. корнями многочлена 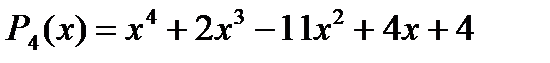. Многочлен P(x) делится на х-1 и на х-2. Значит, Р(х) делится и на их произведение (х-1)(х-2)=х²-3х+2.

Выполним деление углом.

_x⁴ + 2x³ - 11x² + 4x + 4 x²-3x+2

x⁴ - 3x³ + 2x²

_5x³ – 13x² +4х x² + 5x +2

5x³ -15x² + 10x

_ 2x²–6x + 4

2х²- 6х+4

Значит, многочлен Р(х) можно записать в виде

Р(х)=(х-1)(х-2)(х²+5х+2). Итак, первоначальное уравнение равносильно совокупности уравнений х-1=0, х-2=0, х²+5х+2=0.

Решая каждое из этих уравнений, находим решение исходного уравнения: , , .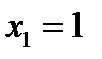

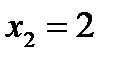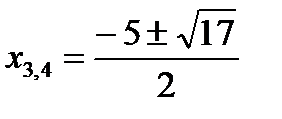2. Рассмотрим два примера на применение метода интервалов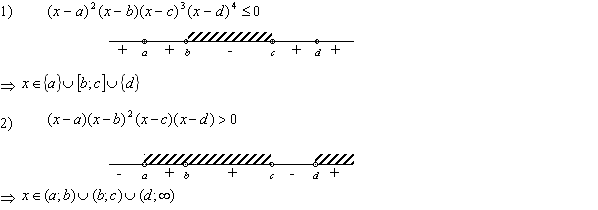

3. Сократите дробь: .

Решение:

Находим нули числителя: х₁=-1 и х₂= .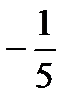

Находим нули знаменателя: х₃=1 и х₄= .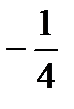

Разложив на множители числитель и знаменатель, получим:

.

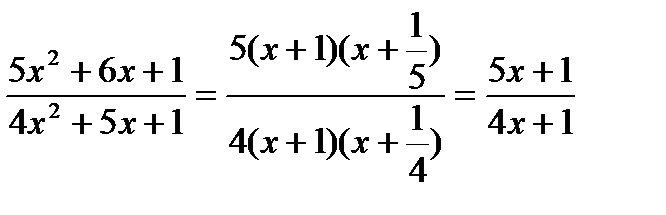6. Изобразить схематически график функции .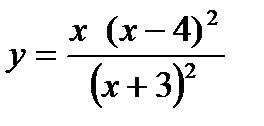

Решение:

Найдем нули числителя и нули знаменателя:

Числитель обращается в ноль в точках х=0 и х=4. Знаменатель обращаетя в ноль при х=-3. Так как на ноль делить нельзя, прямая х=-3 будет являться вертикальной асимптотой графика функции.

Найдем промежутки знакопостоянства:

+

+

+

-

х

у

7. По известным промежуткам знакопостоянства восстановить функцию.

-3

-2

-

-

+

+

-

Решение:

В точках х=5 и х= - 2 функция существует и равна нулю. Это значит, при разложении функции на множители будут присутствовать множители (х-5)²(х+2). Множитель (х-5) записан в квадрате, потому что при переходе через корень х=5

Функция не поменяла свой знак. Но с тем же успехом, вместо второй мы могли использовать любую чётную степень.

Функция не существует при х=-3 и х=2. И при переходе через эти точки функция меняет знак. Это значит, что множители

(х+3) и (х-2) располагаются в знаменателе, причем каждый из них может быть в любой нечетной степени, например (х+3)(х-2)³.

Попытаемся составить функцию: 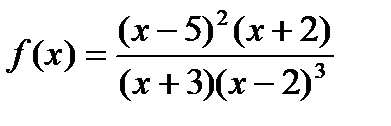, но так как при 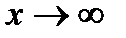составленная нами функция 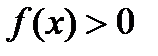, а судя по данным в условии промежуткам знакопостоянства при 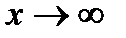, функция должна быть отрицательная, следовательно, мы должны изменить её знак: .

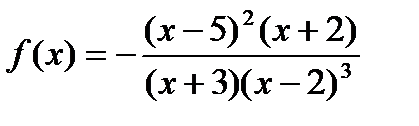Дата добавления: 2015-10-21