Необходимые сведения из теории. Многочленом (полиномом) n-степени с одной переменной называется функция вида Pn(x) = 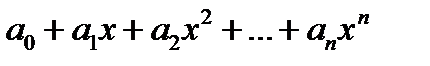(1)

Многочленом (полиномом) n-степени с одной переменной называется функция вида P_n(x) = (1)

где a ₀, a ₁, a ₂, …, a _n-1, a _n - коэффициенты, причем a_n ≠0, .

Два многочлена P_n(x) и Q_n(x) называются равными, если соответственно равны их коэффициенты при одинаковых степенях переменной. Записывают P_n(x) ≡ Q_n(x)

Многочлен P₀(x) ≡ а, где а R, а ≠ 0 считают многочленом нулевой степени.

Многочлен P₁(x) = ax + b, где а ≠ 0 называют линейным двучленом.

Многочлен P₂(x) = ax ² + bx + c, где а ≠ 0 называют квадратным трехчленом

Суммой двух многочленов P_n(x) и Q_m(x) называют многочлен, коэффициенты которого равны сумме соответствующих коэффициентов многочленов Pn (x) и Qm(x).

Разностью двух многочленов P(x) и Q(x) называется многочлен, у которого коэффициенты при каждой степени х равены разности коэффициентов при той же степени в многочленах P(x) и Q(x).

Произведением многочленов P_n(x) = 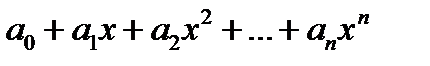an и Q_m(x) = называют многочлен Z_n+m(x)= где , i=0,…,n+m.

Операции сложения и умножения многочленов подчиняются коммутативному, ассоциативному и дистрибутивному законам:

а) коммутативный:

P(x) + Q(x) = Q(x) + P(x); P(x) ∙ Q(x) = Q(x) ∙ P(x);

б) ассоциативный:

P(x) + (Q(x) + Z(x)) = (P(x) + Q(x)) + Z(x);

P(x) ∙ (Q(x) ∙ Z(x)) = (P(x) ∙ Q(x)) ∙ Z(x);

в)дистрибутивный:

P(x) ∙ (Q(x) + Z(x)) = P(x)Q(x) + P(x)Z(x).

Пусть P(x) = Q(x)S(x), P(x) и Q(x) два многочлена, причем степень многочлена P(x) не меньше степени многочлена Q(x) и, если существует такой многочлен S(x), что выполняется равенство

P(x) = Q(x)S(x), то говорят, что многочлен P(x) делится нацело на многочлен Q(x). P(x), Q(x), S(x) называются соответственно делимое, делитель, частное. Если такого многочлена не существует, то многочлен P(x) не делится на Q(x). В этом случае, как и при рассмотрении деления с числами производится деление с остатком.

Разделить многочлен P(x) на Q(x) с остатком это значит представить многочлен P(x) в виде равенства P(x) = Q(x)S(x) + R(x),

где R(x) остаток, причём степень R(x) меньше степени Q(x), причем многочлены S(x) и R(x) находятся однозначно.

Существует теорема Безу, дающая возможность вычислять остаток при делении многочлена на двучлен вида x – с.

Теорема Безу. Остаток от деления многочлена P(x) на двучлен x – с равен значению многочлена P(x) при x = с.

Числоx₀ называется корнем многочлена P(x), если P(x₀) = 0.

Следствие1. Если остаток от деления многочлена P(x) на Q(x) = x – x₀ равен нулю, то значение

x = x₀ есть корень многочлена P(x).

Следствие2. Остаток от деления многочлена P(x) на Q(x) = ax + b равен значению многочлена P(x) при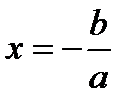

Дата добавления: 2015-10-21