Примеры решения задач. 1. Выполнить деление многочлена P(x) = x4 +4x3 – 4x2 + x + 1 на многочлен Q(x) = x2 +2x + 1 уголком.

1. Выполнить деление многочлена P(x) = x⁴ +4x³ – 4x² + x + 1 на многочлен Q(x) = x² +2x + 1 уголком.

Решение:

Выполним деление углом.

_x⁴ + 4x³ – 4x² + x + 1 x² +2x + 1

x⁴ + 2x³ + x²

_2x³ – 5x² + x x² + 2x – 9

2x³ + 4x² + 2x

_- 9x² – x + 1

- 9x² – 18x – 9

17 x + 10

Процесс деления закончен, так как степень остатка меньше степени делителя. Можно записать:

x⁴ + 4x³ – 4x² + x + 1 = (x² +2x + 1)(x² + 2x – 9) +17 x + 10.

Ответ: x⁴ + 4x³ – 4x² + x + 1 = (x² +2x + 1)(x² + 2x – 9) +17 x + 10.

2. Представить рациональную дробь 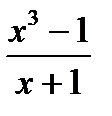в виде суммы целой части и правильной дроби.

Решение:

Выполним деление углом.

_x³ – 1 x + 1

x³ + x² x² – x + 1

_- x² – 1

- x² – x

_x – 1

x + 1

- 2

Отсюда получаем x³ – 1 = (x + 1)(x² – x + 1) – 2. Частное S(x) = x² – x + 1, остаток R(x) = - 2.

Ответ: .

3. Найти частное от деления многочлена P(x)= x⁴ +4x³ – 4x² + x + 1 на многочлен Q(x)=x²+2x+1 методом неопределённых коэффициентов.

Решение:

x⁴ +4x³ – 4x² + x + 1 = (x² +2x + 1)(ax² + bx + c) + dx + e

x⁴ +4x³ – 4x² + x + 1 = ax⁴ +(2a + b)x³ +(c + 2b + a)x² +(b + d + 2c)x + e + c

Приравниваем коэффициенты при одинаковых степенях

Получаем

x⁴ + 4x³ – 4x² + x + 1 = (x² +2x + 1)(x² + 2x – 9) +17 x + 10.

4. Найти остаток от деления многочлена P(x) = x³ + 3x² + 3x + 1 на Q(x) = x – 2

Решение:

На основании теоремы Безу R(x) = P(2) = 8 + 12 + 6 +1 = 27.

5. Найти остаток от деления многочлена P(x) = 3x³ – 2x² + 6x – 4 на Q(x) = 3x – 2

Решение:

На основании теоремы Безу . Значит значение корень многочлена.

Дата добавления: 2015-10-21