
|
Читайте также: |
Натуральной степенью действительного числа  называется действительное число, получаемое в результате умножения числа
называется действительное число, получаемое в результате умножения числа  на себя
на себя 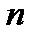 раз
раз  , где
, где  основание степени,
основание степени,  показатель степени (натуральное число).
показатель степени (натуральное число).
Показательной называется функция вида 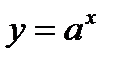 , где
, где  постоянное положительное число отличное от единицы. Ее областью определения является множество всех действительных чисел. Показательная функция монотонно возрастает при
постоянное положительное число отличное от единицы. Ее областью определения является множество всех действительных чисел. Показательная функция монотонно возрастает при  и монотонно убывает при
и монотонно убывает при 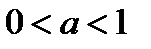 . Для решения практических задач необходимо знать следующие свойства степеней и радикалов:
. Для решения практических задач необходимо знать следующие свойства степеней и радикалов:
1. 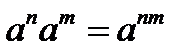
2. 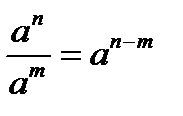
3. 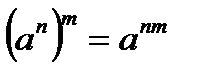
4. 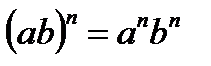
5. 
6. 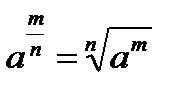
7. 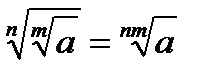
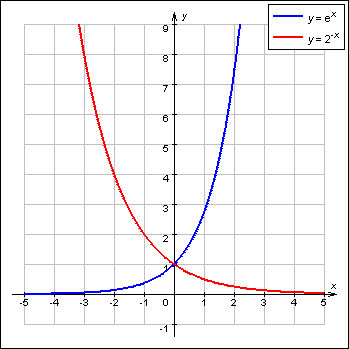
График показательной функции 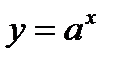 :
:

Пример:
Логарифмом положительного числа  по положительному и не равному единице основанию
по положительному и не равному единице основанию  называется показатель степени, в которую нужно возвести основание
называется показатель степени, в которую нужно возвести основание  , чтобы получить число
, чтобы получить число  . Обозначается
. Обозначается  .
.

Логарифмической называется функция вида  , где а -постоянное положительное число отличное от единицы. Ее областью определения является множество всех положительных чисел (
, где а -постоянное положительное число отличное от единицы. Ее областью определения является множество всех положительных чисел ( ). Логарифмическая функция монотонно возрастает при
). Логарифмическая функция монотонно возрастает при  и монотонно убывает при
и монотонно убывает при 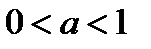 . Показательная и логарифмическая функции являются взаимно обратными. Показательная функция характеризует изменение степени в зависимости от изменения показателя степени, а логарифмическая функция наоборот - изменение показателя степени в зависимости от изменения степени. Свойства логарифмов:
. Показательная и логарифмическая функции являются взаимно обратными. Показательная функция характеризует изменение степени в зависимости от изменения показателя степени, а логарифмическая функция наоборот - изменение показателя степени в зависимости от изменения степени. Свойства логарифмов:
1.Основное логарифмическое тождество:  (
(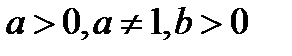 )
)
2. 
3. 
4. 
5. 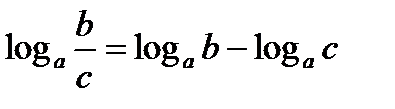
6. 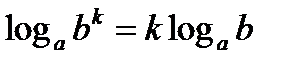
7. 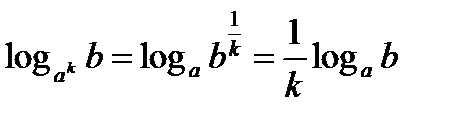
8. 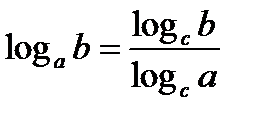 (формула перехода к новому основанию)
(формула перехода к новому основанию)
9. 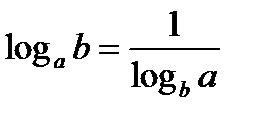
График логарифмической функции:

Пример: Установить соответствие графиков и функций.

Наиболее часто используемыми на практике являются десятичный логарифм 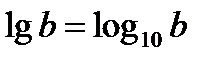 и натуральный логарифм
и натуральный логарифм 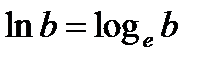
Показательными называются уравнения и неравенства содержащие переменную в показателе степени, а логарифмическими - под знаком логарифма или в основании логарифма. При решении показательных и логарифмических уравнений и неравенств необходимо учитывать следующие правила:
1. Показательное уравнение 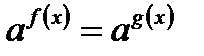 равносильно уравнению
равносильно уравнению 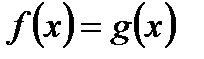 , где
, где  .
.
2. При 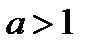 показательное неравенство
показательное неравенство 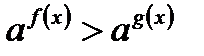 равносильно неравенству
равносильно неравенству  .
.
3. При  показательное неравенство
показательное неравенство 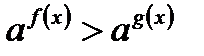 равносильно неравенству
равносильно неравенству 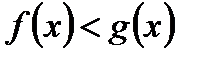 .
.
4. Простейшее логарифмическое уравнение 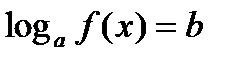 решается потенцированием:
решается потенцированием:

5. Логарифмическое уравнение 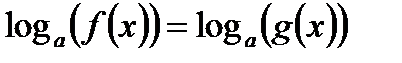 равносильно уравнению
равносильно уравнению 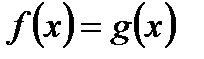 , где
, где 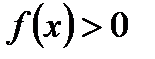 и
и  . Данные неравенства определяют ОДЗ переменной x исходного уравнения, поэтому полученные в результате решения корни уравнения должны удовлетворять этим неравенствам (необходимо делать проверку).
. Данные неравенства определяют ОДЗ переменной x исходного уравнения, поэтому полученные в результате решения корни уравнения должны удовлетворять этим неравенствам (необходимо делать проверку).
6. При 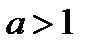 логарифмическое неравенство
логарифмическое неравенство 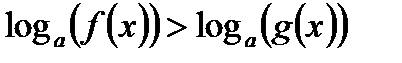 равносильно неравенству
равносильно неравенству 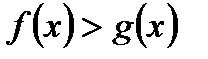 , где
, где 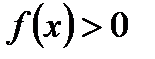 и
и  , т.е. сводится к решению системы
, т.е. сводится к решению системы
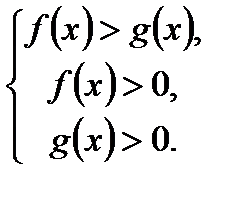
7. При  логарифмическое неравенство
логарифмическое неравенство 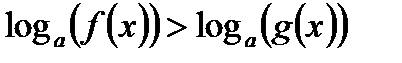 равносильно неравенству
равносильно неравенству  , где
, где 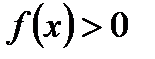 и
и  , т.е. сводится к решению системы
, т.е. сводится к решению системы
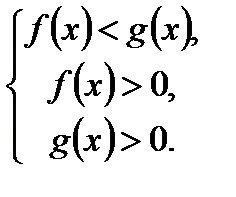
Рассмотрим основные методы решения показательных и логарифмических уравнений.
Дата добавления: 2015-10-21; просмотров: 127 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи для работы в аудитории | | | Методы решения показательных уравнений. |