Основные тригонометрические тождества

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем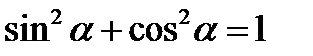

Справедливы тождества:

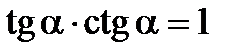
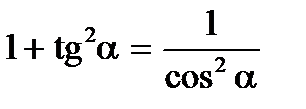
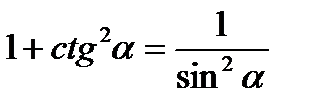
Свойства тригонометрических функций:

периодичность	нечетные функции	ограниченность
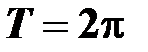
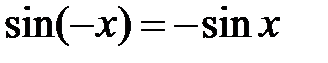
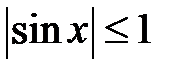
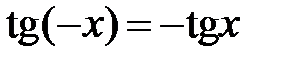
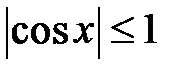
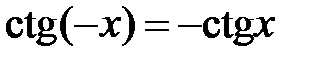
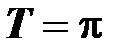
	четная функция	неограниченность
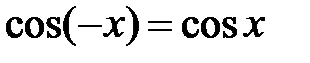
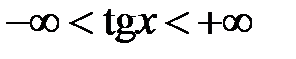
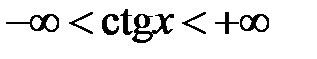
где

Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.

Формулы суммы и разности

.

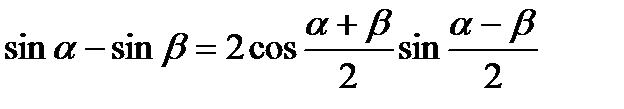
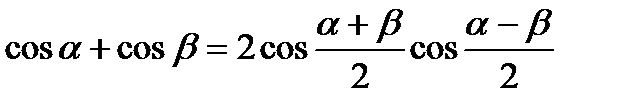
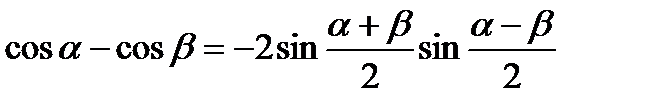
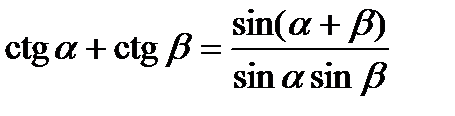
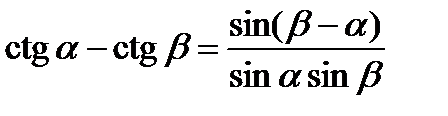
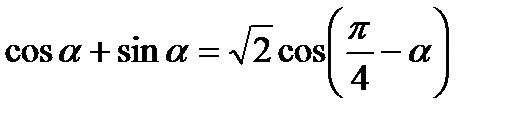
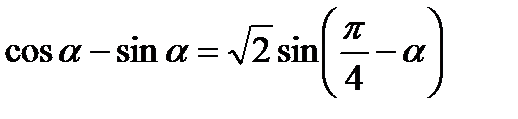
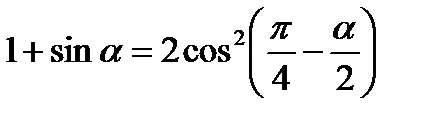
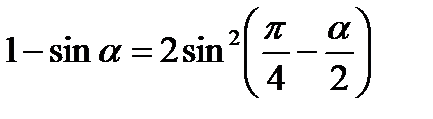Формулы двойного аргумента

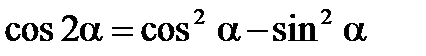
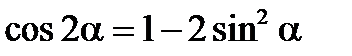
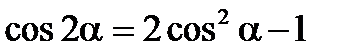
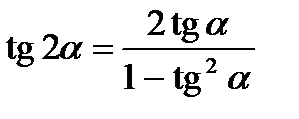
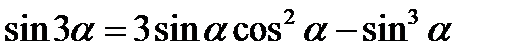
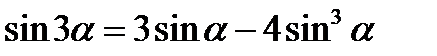
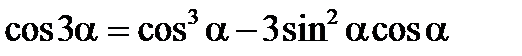
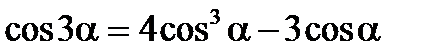
Формулы произведений

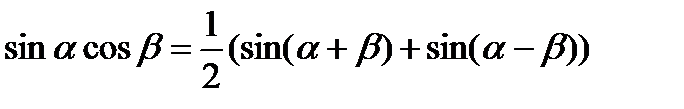
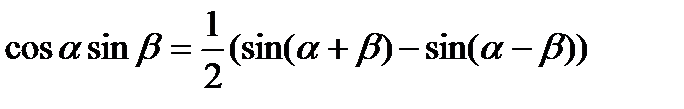
Формулы сложения

; ;

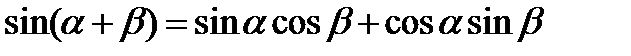
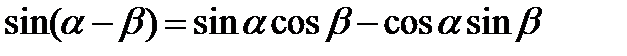
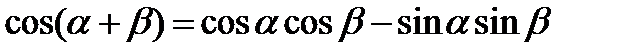
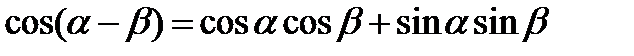
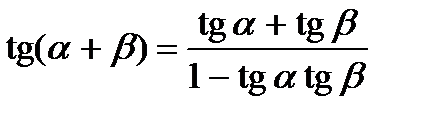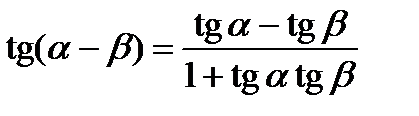
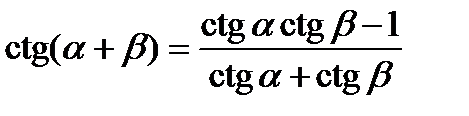Формулы половинного аргумента

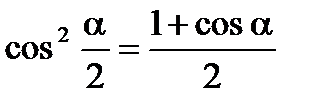
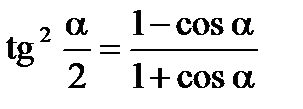
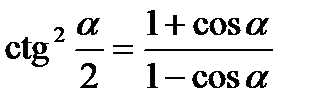
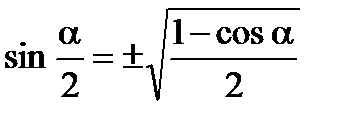
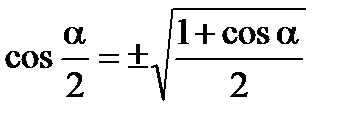
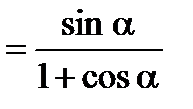
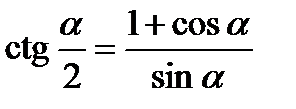
Формулы понижения степени

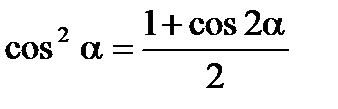
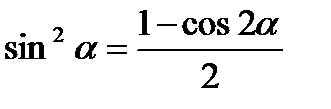
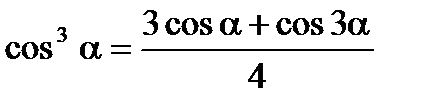
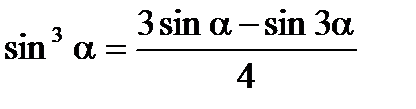
Выражение формул через тангенс половинного угла (тригонометрические подстановки)

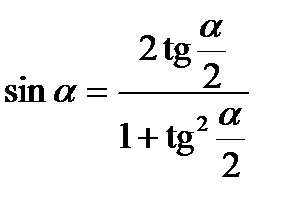
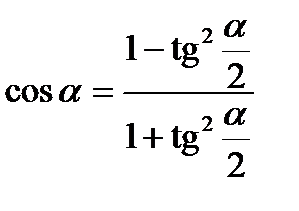
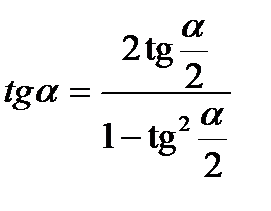
Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений:

; ; ; ;

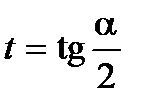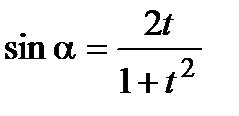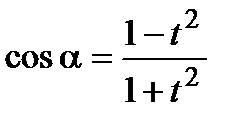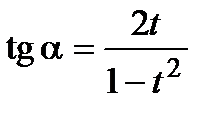Дата добавления: 2015-10-21