Решение. Область допустимых значений: или

Область допустимых значений: или

.

Применим основное логарифмическое тождество. Для этого преобразуем уравнение:

, .

Ответ: 3.

Системы уравнений

Пример. Решить систему уравнений:

Решение

Преобразуем второе уравнение системы, применяя определение логарифма и учитывая, что выражение под знаком логарифма должно быть строго положительным:

Ответ: .

Примеры решения показательных и логарифмических неравенств.

Пример 1. Решить неравенство

Решение: Так как , то получаем или , откуда

; , решая неравенство методом интервалов, получаем

Ответ:

Пример 2. Решить неравенство

Решение: Неравенство равносильно совокупности систем вида

(1) (2)

Система (1) равносильна системе

откуда находим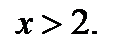

Система (2) равносильна системе

,

откуда следует, что , так как .

Ответ: .

Дата добавления: 2015-10-21