Читайте также:
|
1. 
-это угол, синус которого равен 
. Аналогично определяются 
, 
, 
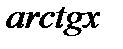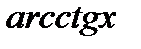. Этифункции обратныфункциям 
, 
, 
, 
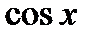. Поэтому они называются обратными тригонометрическими функциями.
Свойства функции :
1) Область определения – промежуток [-1; 1].
2) Множество значений – промежуток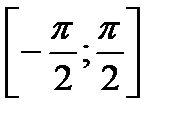 
.
3) Функция нечетная: 
4) Нули функции: 
при 
.
5) Промежутки знакопостоянства:
при 
при 
.
6) Функция возрастает на промежутке [-1; 1]. Она непрерывна и дифференцируема в каждой точке интервала (-1; 1).
7) 
при 
.
8) 
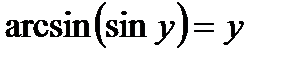при 
.
Рассмотрим функцию 
. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому будем рассматривать отрезок, на котором она строго возрастает и принимает все значения из области значений 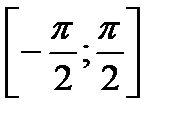. Так как для функции 
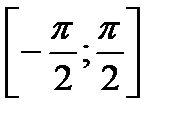на промежутке каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция , график которой симметричен графику функции на отрезке 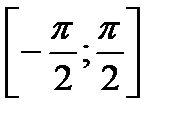относительно прямой 
. Аналогично получаются остальные обратные тригонометрические функции.
График функции :
2. 
Свойства функции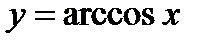 
:
1) Область определения – промежуток [-1; 1].
2) Множество значений – промежуток 
.
3) Функция не является ни четной ни нечетной.
4) Нули функции: 
при 
.
5) Промежутки знакопостоянства:
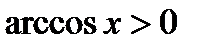при 
6) Функция убывает на промежутке [-1; 1]. Она непрерывна и дифференцируема в каждой точке интервала (-1; 1).
7) 
при .
8) 
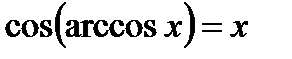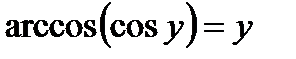при 
.
График функции 
:
3. 
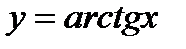
Свойства функции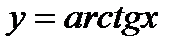 
:
1) Область определения – вся числовая прямая.
2) Множество значений – промежуток 
.
3) Функция нечетная: 
4) Нули функции: 
при 
.
5) Промежутки знакопостоянства:
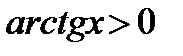при 
при 
.
6) Функция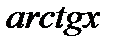 
возрастающая. Она непрерывна и дифференцируема при всех 
.
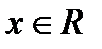7) 
при 
.
8) 
при 
.
График функции 
:
4. 
Свойства функции 
:
1) Область определения – вся числовая прямая.
2) Множество значений – промежуток 
.
3) Функция не является ни четной ни нечетной.
5) Функция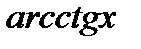 
положительна при всех .
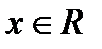6) Функция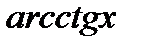 
убывающая. Она непрерывна и дифференцируема при всех .
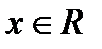7) 
при .
8) 
при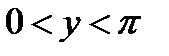 
.
График функции 
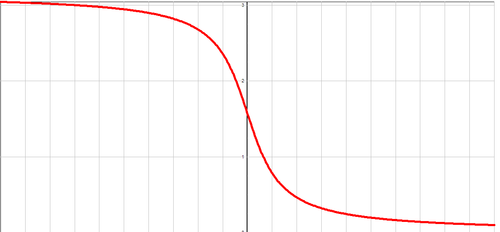
Дата добавления: 2015-10-21; просмотров: 90 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные тригонометрические тождества | | | Виды тригонометрических уравнений и способы их решения |