Асимптоты графика функции.
Определение:
Асимптотой графика функции  называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки  до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат.
Вертикальная асимптота может существовать в точке разрыва или на концах области определения. Если  ,
,  - точка разрыва функции или крайние точки области определения,
- точка разрыва функции или крайние точки области определения,  - вертикальная асимптота.
- вертикальная асимптота.
Горизонтальная асимптота. Если  ,
, 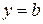 - горизонтальная асимптота.
- горизонтальная асимптота.
Наклонная асимптота имеет вид 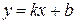
 ,
, 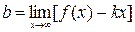
Задания:
Найти асимптоты графика функции:
а)  , б)
, б) 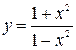
Домашнее задание:
- Для функции
 (на черновике) найти:
(на черновике) найти: - область определения, область значений.
- чётность/нечётность функции, поведение графика функции,
- периодичность функции,
- промежутки возрастания, убывания, экстремумы функции
- промежутки выпуклости, вогнутости, точки перегиба,
- асимптоты.
- Темы для самостоятельного изучения "Уравнение касательной", "Применение дифференциала к приближённым вычислениям"
Литература:
Основные источники:
- Математика: учеб. пособие/В. П. Омельченко, Э. В. Курбатова. - Изд. 7-е, стер. - Ростов н/Д: Феникс, 2013. - 380 с. - (Среднее профессиональное образование).
Дополнительные источники:
- Богомолов Н. В. Практические занятия по математике: учебное пособие для средних учебных заведений – 7-е издание, М.: Высшая школа, 2004
- Гмурман В. Е. Теория вероятностей и математическая статистика: учебное пособие – 12-е изд., - М.: Издательство Юраст, 2010
- Кочетков Е. С. Смергинская С. О., Соколов В. В. Теория вероятностей и математическая статистика – М.: Форум, 2011.
- Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание, стер. – М.: Издательский центр «Академия», 2007
Дата добавления: 2015-10-16; просмотров: 191 | Нарушение авторских прав
Читайте в этой же книге: Сформулируйте определение функции возрастающей (убывающей) на множестве Р. | Применение производной для исследования функции на монотонность и экстремумы. | Применение производной для отыскания наибольших и наименьших величин. |
mybiblioteka.su - 2015-2026 год. (0.003 сек.)

 называется прямая, обладающая тем свойством, что расстояние от точки
называется прямая, обладающая тем свойством, что расстояние от точки  до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат.
до этой прямой стремиться к нулю при неограниченном удалении точки графика от начала координат. ,
,  - точка разрыва функции или крайние точки области определения,
- точка разрыва функции или крайние точки области определения,  - вертикальная асимптота.
- вертикальная асимптота. ,
, 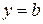 - горизонтальная асимптота.
- горизонтальная асимптота.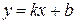
 ,
, 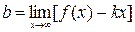
 , б)
, б) 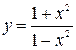
 (на черновике) найти:
(на черновике) найти: