Выпуклость функции. Точки перегиба.

А) б) в)

Г)

Определение:

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла или вогнута.

Теорема: Если вторая производная функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.

Теорема: Вторая производная функции в точке перегиба равна нулю.

Алгоритм исследования функции на выпуклость и точки перегиба.

1) Найти вторую производную функции

2) Найти точки, в которых вторая производная равна нулю или не существует.

3) Исследовать знак второй производной в полученных интервалах,

4) Сделать выводы об интервалах выпуклости и точках перегиба.

5) Найти значения функции в точках перегиба.

Задания:

Найти интервалы выпуклости и точки перегиба графика функции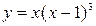

Дата добавления: 2015-10-16