
Читайте также:
|
Определение:
Утверждение 1: Если функция непрерывна на отрезке, то она достигает на нём своего наибольшего и наименьшего значений.
Утверждение 2: Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Утверждение 3: Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции на отрезке
Найти наибольшее и наименьшее значение функции  на отрезке
на отрезке 
1) Найти производную функции 
2) Найти стационарные и критические точки функции, лежащие внутри отрезка  .
.
3) Вычислить значения функции в стационарных, критических точках и на концах отрезка.
4) Выбрать из полученных значений наименьшее и наибольшее.
Задания:
Найти наибольшее и наименьшее значение функции 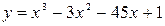
а) на отрезке  ,
,
б) на отрезке  ,
,
в) на отрезке  .
.
Дата добавления: 2015-10-16; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Применение производной для исследования функции на монотонность и экстремумы. | | | Выпуклость функции. Точки перегиба. |