Применение производной для исследования функции на монотонность и экстремумы.

Т-1 (достаточное условие возрастания функции). Если производная функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Т-2 (достаточное условие убывания функции). Если производная функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.

Т-3 Если во всех точках открытого промежутка Х выполняется неравенство 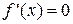, то функция постоянна на промежутке Х

Т-4 Если функция имеет экстремум в точке , то в этой точке производная функции либо равна 0, либо не существует.

Стационарные точки – внутренние точки области определения, в которых производная функции равна 0

Критические точки - внутренние точки области определения, в которых функция непрерывна, но производная не существует.

Т-5 (достаточное условие экстремума). Пусть функция непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку . Тогда:

а) если у этой точки существует такая окрестность, в которой при выполняется неравенство , а при - неравенство , то - точка минимума функции .

б) если у этой точки существует такая окрестность, в которой при выполняется неравенство , а при - неравенство, то - точка максимума функции .

в) если у этой точки существует такая окрестность, что в ней и слева и справа от точки знаки производной одинаковы, то в точке экстремумов нет.

Другими словами: Если при переходе через точку производная функции меняет свой знак с минуса на плюс, то точка - точка минимума функции , а если с плюса на минус – точка максимума.

Алгоритм исследования функции на монотонность и экстремумы:

1) Найти производную функции

2) Найти стационарные и критические точки.

3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.

4) Опираясь на теоремы 1-5 сделать выводы о монотонности функции и экстремумах.

Задания:

Исследовать функцию на монотонность и экстремумы .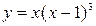

Дата добавления: 2015-10-16