Бесконечно-малые и бесконечно большие функции. Эквивалентность функций.

Рассмотрим ситуацию, когда при и . Такие функции называются бесконечно-малыми. Если существует хотя бы один из двух конечных пределов или , то такие функции называются сравнимыми.

Пусть существует 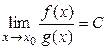, тогда:

а) если , то и - бесконечно-малые одного порядка, в частном случае при функции и - эквивалентные ();

б) если - функция бесконечно-малая более высокого порядка по сравнению с . Если в этом случае существует число , такое что , то - бесконечно-малая порядка r относительно .

Рассмотрим другой случай, когда при и . Такие функции называются бесконечно большими. Пусть , тогда:

а) если , то и бесконечно-большие одного порядка, в частном случае при и называются эквивалентными ();

б) если , то - бесконечно-большая более низкого порядка по сравнению с .

Если в этом случае существует , такое, что , то - бесконечно-большая порядка r по отношению к функции .

Приведем некоторые примеры эквивалентных функций при .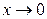

.

Рассмотрим задание.

Найти порядок малости функции относительно функции при . Приведем решение примеров.

Пример 1.24. Найти порядок малости относительно при .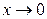

Решение. Рассмотрим . Возможны три случая:

1) , тогда .

2) , тогда .

3) , тогда .

Отсюда следует, что порядок малости .

Пример 1.25. Найти порядок малости относительно при .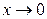

Решение. Рассмотрим

Рассуждая как в предыдущем примере, получим, что .

Дата добавления: 2015-10-21