Замечательные пределы

При вычислении пределов функций часто используются следующие замечательные пределы:

1) - первый замечательный предел;

2) - второй замечательный
предел.

Рассмотрим задание: вычислить предел функции, используя первый или второй замечательный предел.

Приведем решения примеров.

Пример 1.18. .

Решение. Домножим числитель и знаменатель на 5, тогда получим

,

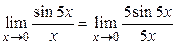но пр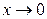и и 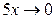, поэтому можно использовать первый замечательный предел:

Пример 1.19. .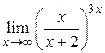

Решение. Прибавим и вычтем в числителе число 2, тогда:

Умножим и разделим показатель 3 х на дробь 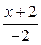, получим:

Задача свелась к нахождению двух пределов: а) и б)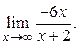

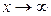В первом пределе обозначим , тогда если , то и . Следовательно, .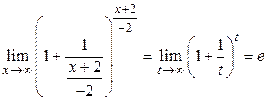

Во втором пределе имеем неопределенность вида . Для ее раскрытия поделим числитель и знаменатель на х:

.

Окончательно получим, что искомый предел равен .

Пример 1.20. .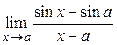

Решение. Преобразуем числитель по формуле разности синусов, тогда получим:

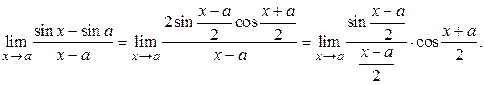
Если , то и, следовательно, 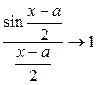в силу первого замечательного предела, а 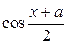при стремится к

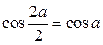. Поэтому .

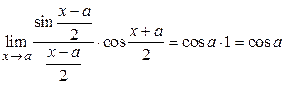Пример 1.21. .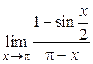

Решение. Заменим 1 на и применим формулу разности синусов, получим:

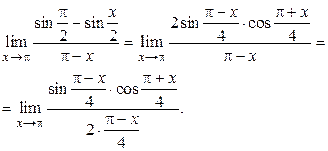
При 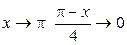, следовательно, выражение при 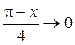на основании первого замечательного предела, а 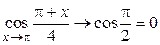. Окончательно получим, что искомый предел равен

Пример 1.22.

Решение. Прибавим и вычтем в числителе число 5, тогда: 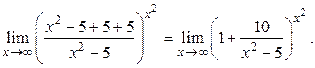Умножим и разделим показатель х ² на дробь получим:

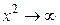Если , то 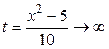. Следовательно,

,
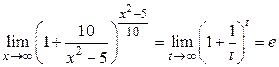а .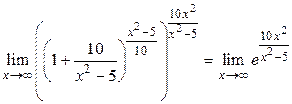

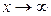Как будет показано ниже, в силу непрерывности экспоненты . Показатель при является неопределенным выражением вида . Его предел равен . Окончательно получим, что искомый предел равен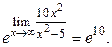

Пример 1.23.

Решение. Заменим по формуле половинного угла: , тогда .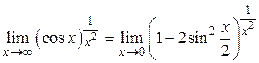
Умножим и разделим показатель на 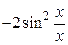, получим: . По аналогии с предыдущим примером выделим в этом выражении второй замечательный предел, тогда а

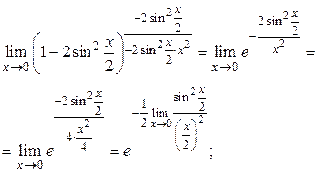
, как следствие из первого замечательного предела, следовательно, окончательно получим:

Дата добавления: 2015-10-21