Вычисление предела функции с помощью теоремы об арифметических свойствах предела. Раскрытие неопределенностей

Теорема 5 (об арифметических свойствах предела). Пусть , , где A и B - конечные числа; C = const. Тогда:

1) ;

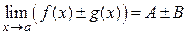2) ;

3) 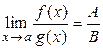при условии, что B ¹ 0;

4)

5)

В определении значения a и A могут быть как конечными числами, так и символами . В последнем случае в процессе вычисления пределов могут возникать неопределенные выражения. Для вычисления предела сначала нужно преобразовать исходные выражения, а затем уже применить теорему 5.

Рассмотрим задание: вычислить пределы функций, раскрыв неопределенности вида .

Приведем решения примеров.

Пример 1.14.

Решение. Числитель и знаменатель стремятся к нулю. Имеем неопределенность вида 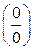. Разложим числитель как сумму кубов, чтобы выделить множитель, создающий неопределенность, получим:

.

Мы видим, что таким множителем является . Проведем сокращение на (x + 1), после этого можно применить теорему 5:

Пример 1.15.

Решение. Числитель и знаменатель стремятся к бесконечности. Имеем неопределенность вида . Разделим числитель и знаменатель на x, получим:

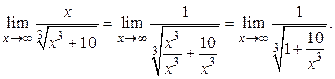
Теперь можно применить теорему 5, так как пределы числителя и знаменателя конечны:

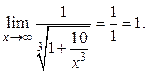
Пример 1.16.

Решение. Уменьшаемое и вычитаемое стремятся к бесконечности. Имеем неопределенность вида . Преобразуем исходное выражение, приведя его к общему знаменателю и разложив знаменатель на множители:

После сокращения на (x – 1) можно применить теорему 5:

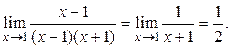
Пример 1.17.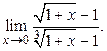

Решение. Числитель и знаменатель стремятся к нулю. Имеем неопределенность вида 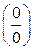. Домножим числитель и знаменатель на сумму 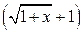и на неполный квадрат суммы , получим:

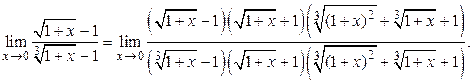
Произведение первого и третьего сомножителей знаменателя даст разность кубов, а произведение первого и второго сомножителей числителя даст разность квадратов, что позволяет упростить выражение и применить теорему 5:

Дата добавления: 2015-10-21