Виды тригонометрических уравнений и способы их решения

Уравнени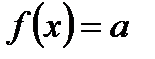е , где 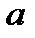– данное число, а – одна из основных тригонометрических функций, называют простейшим тригонометрическим уравнением.

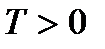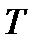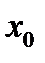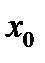
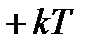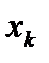
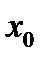
Простейшее тригонометрическое уравнение имеет период , если функция имеет период . Если для некоторого простейшего тригонометрического уравнения с периодом найдено некоторое решение , то любое число при любом целом также является решением этого уравнения. Множество всех решений вида , где пробегает все целые числа, называют серией решений этого уравнения и записывают в виде , .

Видами тригонометрических уравнений простейшего типа являются: , , , .

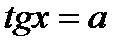1.Уравнение .

Так как областью значений синуса является отрезок , то это уравнение не имеет решений при 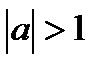. Пусть теперь . Построим на одном чертеже графики функций и .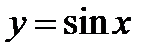

y

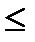
По рисунку ясно, что прямая пересечет синусоиду бесконечно много раз. Это означает, что при 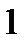уравнение имеет бесконечно много корней. Так как синус имеет период 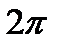, то достаточно найти все решения в пределах этого периода. По графику видно, что при 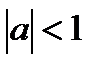на отрезке есть два числа (угла) синус которых равен .

Если один из таких углов , то тоже решение уравнения , причем углы 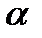и 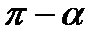не получаются один из другого прибавлением периода .

Пусть - какое либо решение уравнения 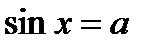, где . Тогда все решения этого уравнения получаются по формулам , , .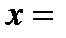

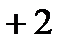
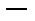
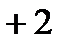
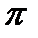
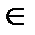
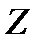Эти две серии решений иногда записываются одной формулой:

(-1) ,

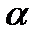
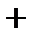
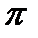
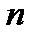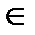
Уравнение при 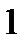имеет бесконечно много решений. Для одного из них имеется специальное название – арксинус.

Пусть число a по модулю не превосходит единицы.

Арксинусом числа a называется угол x, лежащий в пределах от 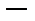до 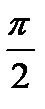, синус которого равен a.

Обозначение: .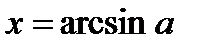

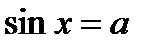Равенство равносильно двум условиям: и .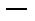

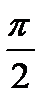
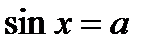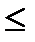
Решения уравнения (при ) можно записать так:

, ,

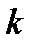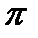
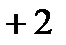
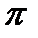
или в виде одной формулы:

2. Уравнение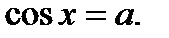

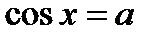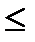
При уравнение решений не имеет; если , то решений уравнения бесконечно много.

y

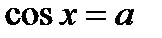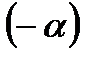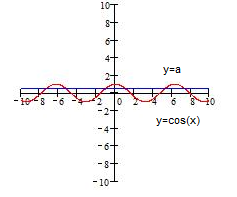
Если – какое-либо решение уравнения , то также есть решение этого уравнения, так как . На графике видно, что при 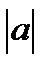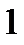в пределах одного периода уравнение имеет два решения.

x

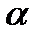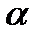
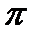
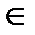
Если - одно из решений уравнения , то все решения исчерпываются двумя сериями решений:

, и , .

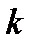
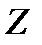Эти серии записывают в виде одной формулы: , .

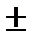
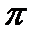
Также как и для синуса, выделяется одно определенное решение уравнения 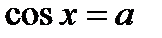и ему дается специальное название – арккосинус.

Пусть – число, по модулю не превосходящее единицы.

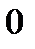Арккосинусом числа называется угол , лежащий в пределах от до , косинус которого равен .

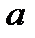Обозначение: .

Равенство равносильно двум условиям:

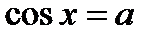и 0 .

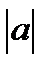
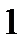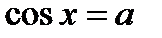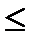
Арккосинус числа существует лишь при . Решение уравнения (при ) можно записать в общем виде:

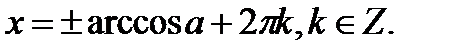
3. Уравнения Область значений тангенса (котангенса) – вся числовая ось. Поэтому уравнения 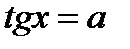, 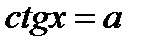имеют решения при любом 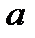. В пределах одного периода тангенс и котангенс принимают каждое значение ровно один раз. Поэтому если известно одно решение уравнения 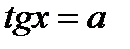или 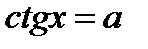, то все остальные получают прибавление периода:

, , ;

, , .

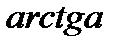
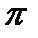
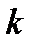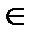
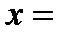
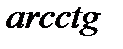
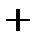
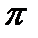
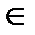
Арктангенсом числа 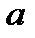называется угол , тангенс которого равен .

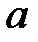Обозначение: .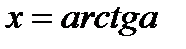

Уравнение равносильно двум условиям:

и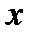

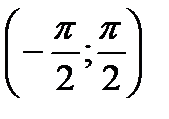
Общая формула:

Арккотангенсом числа называется угол 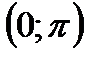, котангенс которого равен .

Обозначение: .

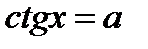Уравнение равносильно двум условиям: и ; ,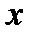

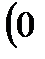Общая формула:

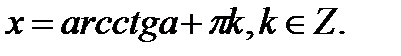
Решения простейших тригонометрических уравнений:

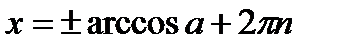; , где

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; ;

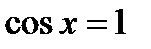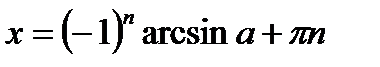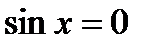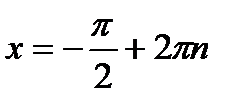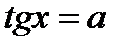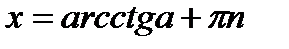Дата добавления: 2015-10-21