Тригонометрические неравенства

Два тригонометрических выражения, соединенных между собой знаками «>» или «<», называются тригонометрическими неравенствами.

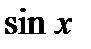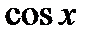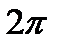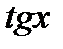Решить тригонометрическое неравенство – это значит найти множество значений неизвестных, входящих в неравенство, при которых оно выполняется. Тригонометрические функции и имеют наименьший положительный период , а и 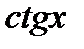имеют наименьший положительных период 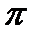. При решении неравенств с тригонометрическими функциями следует использовать периодичность этих функций и их монотонность на соответствующих промежутках.

Для того, чтобы решить неравенство, содержащее только 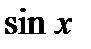или только 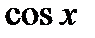, достаточно решить это неравенство на каком-либо отрезке длины 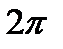. Множество всех решений получим, прибавив к каждому из найденных на этом отрезке решений числа вида 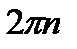, где . Для неравенств, содержащих тольк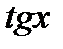о и , решения находятся в промежутке длиной 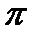, а множество всех решений получим, прибавив к каждому из найденных на этом отрезке решений числа вида 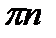, где .

Тригонометрические неравенства можно решать, прибегая к графикам функций 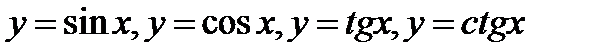или пользуясь единичной окружностью.

Чтобы решить простейшее тригонометрическое неравенство нужно:

1. Провести прямую к линии соответствующей функции.

2. Выделить дугу, на которой лежат решения неравенства.

3. Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.

4. Прибавить к концам интервала числа, кратные периоду функции.

Дата добавления: 2015-10-21