Целесообразно решать тригонометрические неравенства методом интервалов.

Метод интервалов основан на свойстве непрерывных функций. Одним из важных свойств является свойство знакопостоянства непрерывной функции: если на интервале функция непрерывна и не обращается в 0, то на этом интервале она сохраняет постоянный знак.

Алгоритм решения неравенств методом интервалов:

1. Находим область определения функции , где – непрерывная функция в любой точке .
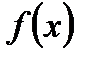2. Решая уравнение , находим нули функции. Корни уравнения принадлежащие разбивают ее на промежутки, на каждом из которых непрерывная функция не обращается в нуль, значит, знакопостоянна.
3. Наносим и нули функции на числовую прямую.
4. Исследуем и рассматриваем знаки функции на каждом из промежутков.
5. С учетом знака неравенства записываем ответ.

При решении тригонометрических неравенств вида 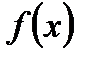>0 или 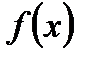<0, где 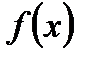– периодическая функция с периодом Т, следует сначала решить его на одном периоде, например, для , а затем получившее решение периодически продолжить.

Пример1: Неравенство на интервале является простейшим типовым неравенством. Для его решения наиболее наглядно использование рисунка:

Ответ:

Пример2: Неравенство нужно преобразовать к однородному виду:

Применяем формулу

или 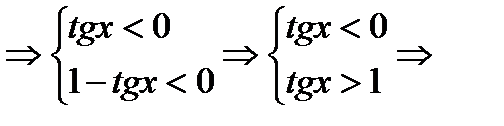система решений не имеет

Ответ: .

Дата добавления: 2015-10-21