Решение. Дифференциальное уравнение нагрева однородного тела

Дифференциальное уравнение нагрева однородного тела

где n = 1 + m. По условию задачи принято m= 0,25 и m = 1,00.

На рис.1 представлена «электрическая схема», в которой электрические переходные процессы описываются дифференциальным уравнением подобному дифференциальному уравнению нагрева однородного тела.

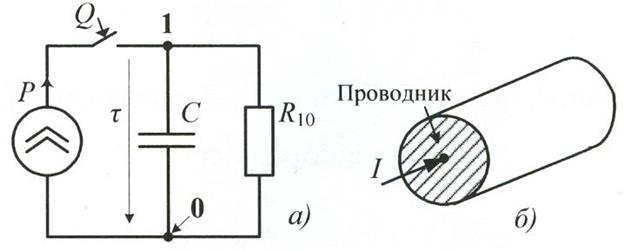
Рис.1. «Электрическая схема» теплового переходного процесса нагрева однородного тела (а) и моделируемое однородное тело (б) – проводник.

P = I²R – выделяемая в проводнике током Iмощность потерь, где R–значение сопротивления проводника;

Q – выключатель, обеспечивающий возникновение переходного процесса; 1 – точка «высокого потенциала», соответствующая в нагреваемом проводнике текущей температуре θ; τ = (θ-θ₀) – «разность потенциалов» между точкой «высокого потенциала» θ и точкой «нулевого потенциала» - 0, соответствующей температуре окружающей среды θ₀; С – общая теплоёмкость проводника;

– тепловое сопротивление окружающей среды.

Дифференциальное уравнение адиабатического нагрева однородного тела:

На рис.2 представлена «электрическая схема», в которой электрические переходные процессы описываются дифференциальным уравнением подобному дифференциальному уравнению адиабатического нагрева однородного тела.

Рис.2. «Электрическая схема» теплового переходного процесса адиабатического нагрева однородного тела (а) и моделируемое однородное тело (б) – проводник.

Дата добавления: 2015-10-21