Решение уравнения адиабатического нагрева

Цель задачи.

Есть примеры, в которых рассматривается исключительно адиабатический режим нагрева. Поэтому необходимо получение с «нуля» адиабатического нагрева. Это одна причина вывода адиабатического нагрева.

Другая цель. Дифференциальное уравнение получается в этом случае простейшее. Простота дифференциального уравнения приводит к тому, что мы можем сразу получить дифференциал превышения температуры dτв явном виде. Он необходим для начального демонстрирования дифференциального исчисления.

Уравнение адиабатического нагрева однородного тела имеет вид:

(1)

где P = I²R – выделяемая мощность, (Вт)

здесь I = const– действующее значение тока;

R = const– значение сопротивления проводника;

С₀ = cV– общая теплоёмкость однородного проводника,

здесь с – удельная объёмная теплоёмкость проводника ;

V – объем проводника, [м³];

τ = (θ -θ₀) – текущее превышение температуры однородного тела;

здесь θ – температура однородного тела;

θ₀ – температура окружающей среды.

При выводе уравнения нагрева однородного тела предполагалось, что его длина lдостаточно большая и тепловое состояние на конце не оказывает влияние на тепловые процессы однородного тела.

Прежде чем интегрировать уравнение (1) произведем размерный анализ.

Разделим обе части уравнения (1) на С₀

(2)

Размерность имеет вид:

Для уравнения имеем:

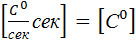
Уравнение (2) неудобно для анализа. Если бы удалось выразить значение через параметры переходного режима, то анализ уравнения был бы очень простым, а главное наглядным

Наглядность уравнения невозможно получить без решения уравнения нагрева с учетом теплоотдачи. Кроме того, адиабатический нагрев – это абстракция. На самом деле его не существует.

Далее приводится решение общего уравнения нагрева с учетом теплоотдачи и показано, что

(3)

где

– установившееся значение превышения температуры при выделяемой мощности Р;

Т – постоянная времени нагрева.

С учётом (3) уравнение (2) будем иметь вид

или

Проинтегрируем последнее уравнение и получим общий интеграл

(4)

где С – постоянная времени интегрирования, определяемая из начальных условий при t = 0, τ = τ_нач.

Подставим в (4) начальные условия. Получим

Частный интеграл уравнения (4) будет иметь вид

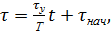(5)

где τ_у = (θ_у − θ₀) – установившееся превышение температуры;

здесь θ_у – установившаяся температура однородного тела, а θ₀ – температура окружающей среды. Если бы дали нагреться телу

или

,

здесьk_T – коэффициент теплоотдачи с боковой стенкой однородного тела;

F – площадка боковой стенки однородного тела.

τ_нач = (θ_нач − θ₀) – начальное превышение температуры над температурой окружающей среды,

здесь θ_нач – начальное значение температуры и θ₀ – температура окружающей среды;

t− время нагрева и для адиабатического режима оно не должно превышать t ≤ 0,05T. При больших значениях t уравнение попросту несправедливо.

Примечание1: τ ≤τ_у – то есть, превышение температуры не может быть больше установившегося превышения, если бы телу дали нагреться.

Отсюда следует вывод. t ≤ Tпри адиабатическом процессе нагрева.

Если t = T, то τ_нач не будет играть роли (надо проверить расчетами).

Примечание 2: Уравнение (5) нельзя получать отдельно от общего уравнения нагрева. Поэтому, при рассмотрении адиабатического режима обязательно надо знать решение общего уравнения нагрева однородного тела.

Примечание 3: Уравнение (5) имеет странное значение текущего превышения: При t = 0,τ = τ_нач – все верно. На самом деле так оно и есть. Другое дело при t = T,τ =τ_у + τ_нач, что является неверным. Реально адиабатический режим имеет место при t ≤ 0,05T. Именно при таких значениях времени (5) справедливо и применимо. Ошибка в значение τ при этом не превышает 5 %. Что очень важно нашли фактическую границу начала адиабатического режима.

Решение дифференциального уравнения адиабатического нагрева в форме (5) выражено через значение превышения температур τ_у и τ_нач. Условно решение в форме (5) можно назвать «температурным».

Желательно иметь форму уравнения в котором фигурируют не выходные характеристики режима нагрева, а входные характеристики – значения токов, которые определяют значения τ_нач и τ_у. Иными словами необходимо получить «токовую» форму уравнения (5).

Ранее было получено соотношение:

(6)

где P = I²R – выделяемая мощность в однородном теле;

τ_у = θ_у – θ₀ – установившееся превышение температуры над температурой окружающей среды θ₀.

Определим зависимость τ_у = f (k), где k – кратность тока I: k = , где I_ном – номинальный ток.

Установившееся превышение температуры при номинальном токе известно из нормативной документации и соответствует номинальному превышению температуры:

, (7)

где τ_н = (θ_н – θ₀) – номинальное превышение температуры над температурой окружающей среды θ₀, но не θ_0н.

I_н – номинальный ток при температуре окружающей среды θ₀.

Разделим (6) на (7) и получим:

τ_у = τ_нk², (8)

где k – кратность тока Iпо отношению к номинальному тока I_н;

τ_н = (θ_н − θ_0н) – номинальное превышение температуры при протекании тока I_н;

здесь θ_н – номинальное значение температуры;

θ_0н – номинальное значение температуры окружающей среды.

По аналогии с τ_у можно выразить начальное превышение температуры τ _нач через номинальное превышение температуры:

τ_нач= (9)

где R_нач = 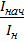– кратность начального тока I_нач по отношению к номинальному току I_н.

Подставим (8) и (9) в уравнение (5) и получим:

;

(10)

где – кратность тока по отношению к номинальному току;

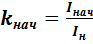– начальная кратность тока.

t ≤ 0,05T – время протекания тока, при котором формула (10 справедлива.

Выражение (10) позволяется определить ВТХ, если задаться допустимым превышением температуры τ_нач при коротком замыкании:τ_нач = θ_кз − θ₀.

.

По аналогии заменим τ_нач через соответствующий ток τ_нач = , где . Тогда имеем

Преобразуем последнее выражение относительно и получим ВТХ

. (11)

Учитывая, что ≤ 0,05 легко определить значение k.

Вывод.

Был рассмотрен адиабатический процесс нагрева неоднородного тела. Получено уравнение этого процесса и решение его в общем виде с помощью систем компьютерной графики Derive и Mathcad. Произведено сравнение с адиабатическим процессом нагрева однородного тела.

В случае однородного тела теплообмен идет только между проводником и изоляцией (окружающей средой). И передача тепла идет, равно как и нагрев, равномерно в любой точке тела, т.е. проводник идеально гладкий. Такой теплообмен считается идеальным. В реальном же случае, в случае неоднородного тела, теплообмен происходит неравномерно ввиду «не идеальности» (не абсолютно гладкие) изоляции и проводника. Так же в реальном случае имеет место тепловое сопротивление, как проводника, так и изоляции, что тоже вносит неравномерность в процесс нагрева. Соответственно время нагрева в случае однородного тела меньше, чем время нагрева в случае реального (неоднородного) тела.

Дата добавления: 2015-10-21