Решение данных уравнений

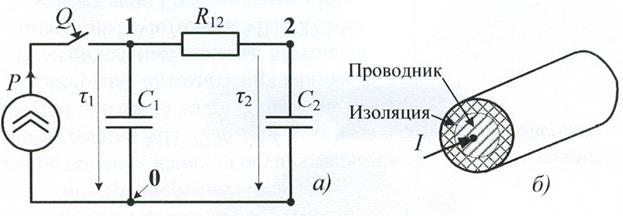
Рис.2. «Электрическая схема» теплового переходного процесса адиабатического нагрева неоднородного тела (а) и моделируемое неоднородное тело (б) – проводник.

Р = I²R– выделяемая в проводнике током Iмощность потерь, где R– значение сопротивления проводника;

Q– выключатель, обеспечивающий возникновение переходного процесса; 1– точка «высокого потенциала», соответствующая в нагреваемом проводнике текущей температуре θ_ж; τ₁ = (θ_ж – θ₀) – «разность потенциалов» между точкой «высокого потенциала проводника (жилы)» θ_ж и точкой «нулевого потенциала» - 0, соответствующей температуре окружающей среды θ₀; С₁ – общая теплоемкость проводника; 2 – точка «высокого потенциала изоляции», соответствующая в нагреваемом проводнике текущей температуре θ_из и точкой «нулевого потенциала» - 0, соответствующей температуре окружающей среды θ₀; С₂ – общая теплоемкость изоляции; – тепловое сопротивление изоляции.

Система дифференциальных уравнений, соответствующая адиабатическому нагреву

;

,

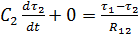где W = I²R.

Преобразуем эту систему уравнений, получим

Введем следующие параметры процесса:

T₁ = R₁₂C₁; T₂ = R₁₂C₂; d = .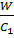

С учетом принятых обозначений система примет вид

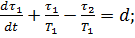
Для решения системы используем операторный метод.

Найдем изображение системы

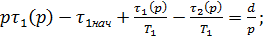
Преобразуем систему

Эта система представляет собой систему алгебраических уравнений. Решаем её с помощью системы компьютерной математики Derive.

1. Решение системы двух уравнений (адиабатический нагрев неоднородного тела с постоянными параметрами С1, С2, P=I²R)

(p+1/T1)τ1(p) - (1/T2)τ2(p) = D/p+τ1нач

- (1/T2)τ1(p) + (p+1/T2)τ2(p) = τ2нач

1.1. Решение системы двух уравнений с помощью оператора “solve”

#2: SOLVE([( ], [τ1s, τ2s])

#3: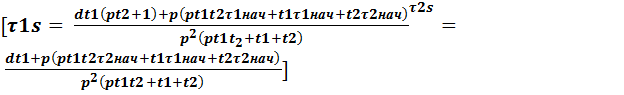

2. Преобразование τ1sи τ2sдля последующего получения оригинала указанных температур с помощью команд соответственно “Expand” и “Factor”

#4:

#5:

#6: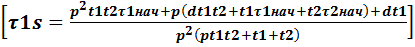

#7:

#8:

#9:

Mathcad

Дата добавления: 2015-10-21