Задачи для работы в аудитории. 1. Известно, что при любом 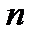сумма членов некоторой арифметической прогрессий

1. Известно, что при любом сумма 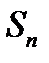членов некоторой арифметической прогрессий выражается формулой . Найти первые три члена этой прогрессий.

2. Сумма всех членов бесконечно убывающей геометрической прогрессии равна 6, а сумма их квадратов равна 7,2. Найти знаменатель прогрессии.

3. Третий и седьмой члены арифметической прогрессии равны 1,1 и 2,3. Найти сумму десяти первых ее членов.

4. Три числа дают в сумме 18 и образуют арифметическую прогрессию. Если к ним прибавить соответственно 1, 3 и 17, то они составляют возрастающую геометрическую прогрессию. Найти исходное третье число.

5. Сумма третьего и седьмого членов арифметической прогрессии равна 8, а их произведение равно 15. Найти сумму первых двадцати членов этой прогрессии.

6. Сумма первого и четвертого членов геометрической прогрессии равна 40, а сумма второго и пятого равна 10. Найти знаменатель прогрессии.

Ответы к задачам для работы в аудитории

1. 1; 9; 17.

2.

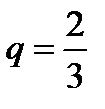
3.

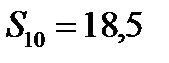
4. .

5. 135 или 25.

6. 0,25.

Дата добавления: 2015-10-21