Примеры решения задач

Задача 1. Найти сумму первых 20 членов арифметической прогрессии, если ее первый член равен 2, а седьмой равен 20.

Решение. Используя условие задачи и формулу для n -го члена арифметической прогрессии, получим:

и .

Отсюда найдем разность прогрессии:

.

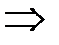
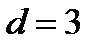Воспользуемся формулой для суммы первых n членов арифметической прогрессии:

.

Тогда получим: .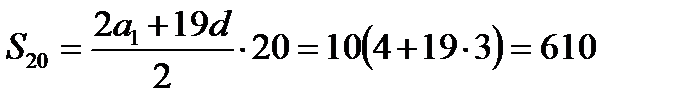

Ответ: .

Задача 2. Произведение второго и восьмого членов арифметической прогрессии равно 64, а их сумма равна 20. Определить порядковый номер члена этой прогрессии, равного 6.

Решение. Обозначим:

– первый член арифметической прогрессии,

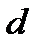– разность прогрессии.

Тогда 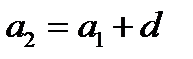и .

Из условия следует:

Из второго уравнения:

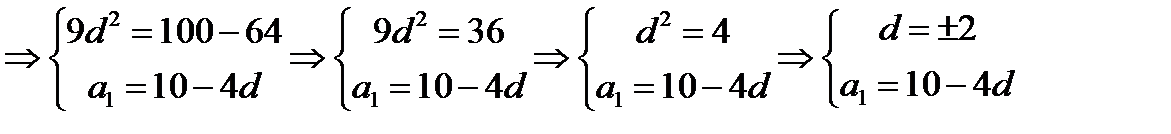
1) Если , тогда

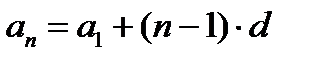, по условию , поэтому:

2) Если , тогда

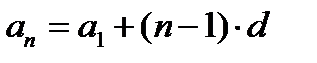, по условию , поэтому:

Ответ: .

Решение данной задачи можно проверить, записав две арифметические прогрессии, и убедится в выполнении условий задачи:

1) 2; 4; 6; 8; 10; 12; 14; 16; 18; …

2) 18; 16; 14; 12; 10; 8; 6; 4; 2; 0; –2; …

Задача 3 Три числа, сумма которых равна 78, образуют геометрическую прогрессию. Их можно рассматривать также как первый, третий и девятый члены арифметической прогрессии. Найти эти числа.

Решение:

Пусть числа 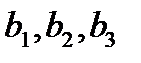- члены геометрической прогрессии, - члены арифметической прогрессии. Тогда , 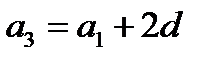. Имеем систему уравнений:

,

,

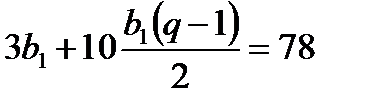=78,

,

,

, ,

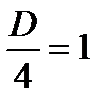не удовлетворяет;

,

,

,

.

Ответ:

Задача 4. Найти 4 числа, составляющие геометрическую прогрессию, в которой сумма крайних членов равна 27, а произведение средних равно 72.

Решение. Имеются четыре числа: . Известно, что 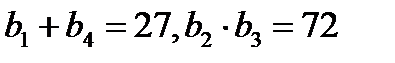. Воспользовавшись формулой общего члена геометрической прогрессии, получим, что . Из второго уравнения

, что можно подставить в первое уравнение и получить:

, откуда следует квадратное уравнение

, корнями которого являются числа 24 и 3. Находя , мы получим два набора чисел - первый начинается с 24: и соответствует , второй - , где .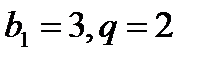
Ответ: или .

Задача 5. В геометрической прогрессии сумма первых трех членов равна 9, а сумма первых шести членов равна (- 63). Найти сумму первых десяти членов прогрессии.

Решение. По условию задачи ; , откуда 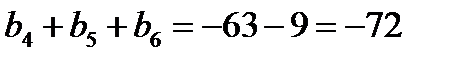и, подставляя формулы членов геометрической прогрессии, находим . Найдем теперь :

и , откуда окончательно: .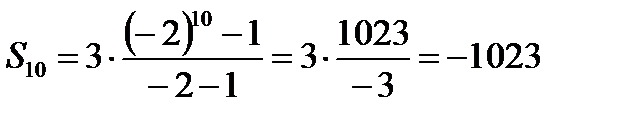

Ответ: .

Задача 6 Сумма бесконечно убывающей геометрической прогрессии равна 4, а сумма кубов её членов равна 192. Найти первый член и знаменатель прогрессии

Дата добавления: 2015-10-21