
Читайте также:
|
1. Решить уравнение а)  .
.
Решение:
Воспользуемся геометрическим смыслом модуля: решением уравнения будут являться точки х такие, что расстояние от точки х до точки смены знака модуля (точки х=3) равно 5.
| +5 |
| -5 |
| -2 |
Ответ: х=-2; х=8.
б) Решить уравнение  .
.
Решение:
Построим графики функций у=  и у=3.
и у=3.

Найдем абсциссы их точек пересечения: х=-1 и х=5.
Ответ: х=-1 и х=5.
2. Решить уравнение 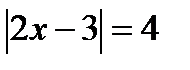 .
.
Решение:
На расстоянии 4 от точки х на координатной прямой лежат две точки: -1 и 7, а 2х есть одна из них.
| +4 |
| -4 |
| -1 |
Следовательно, 2х=-1 или 2х=7, так что заданное уравнение имеет 2 корня:  и
и  .
.
Также можно было, разделив обе части уравнения на 2, получить уравнение вида  . И воспользоваться геометрическим смыслом модуля: решением уравнения являются точки х такие, что расстояние от точек х до точки смены знака модуля (точки х=
. И воспользоваться геометрическим смыслом модуля: решением уравнения являются точки х такие, что расстояние от точек х до точки смены знака модуля (точки х=  ) равно 2.
) равно 2.
| +2 |
| -2 |




Ответ: х=  , х=
, х=  .
.
3. Решить неравенство  .
.
Решение:
Разделим обе части неравенства на 3 и перейдем к равносильному неравенству  , геометрический смысл которого состоит в нахождении точек х, расстояния от которых до точки
, геометрический смысл которого состоит в нахождении точек х, расстояния от которых до точки  больше
больше
чем  .
.


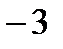



Ответ:  .
.
4. Решить уравнение  .
.
Решение:
На равном расстоянии от точек -6 и 2 лежит единственная точка- середина отрезка 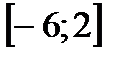 , т.е. х=-2. Это и есть единственный корень данного уравнения.
, т.е. х=-2. Это и есть единственный корень данного уравнения.
Ответ: х=-2.
5. Решить уравнение 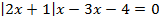 .
.
Решение:
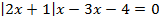

 .
.
Ответ: х=2.
6. Решить уравнение  .
.
Решение:
1. Вычислим нули подмодульных выражений:
 ;
;  ;
;  ;
; 
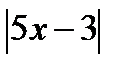
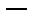


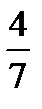







Ответ:  .
.
7. Решите уравнение  , выбрав наиболее рациональную схему для решения:
, выбрав наиболее рациональную схему для решения:
1. 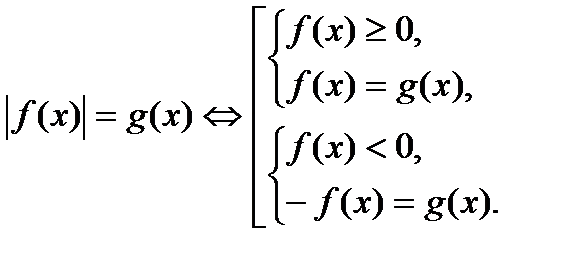
2. 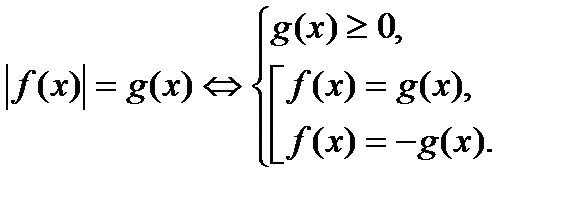
Решение:
Вторая схема проще т. к. предполагает решение линейного неравенства, в отличие от первой, где пришлось бы решить два квадратных неравенства.
2) 








Ответ: -3;-2;0.
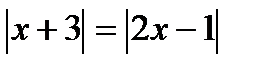
Решение:


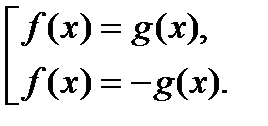


Ответ:  .
.

Решение:



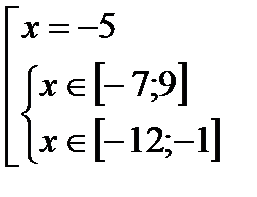
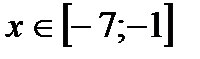
Ответ:  .
.
10. 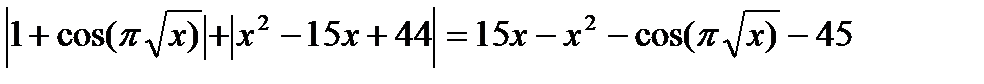
Решение:
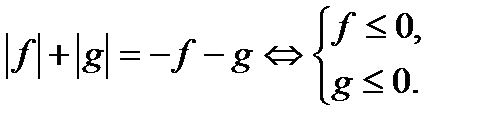

 x=9
x=9
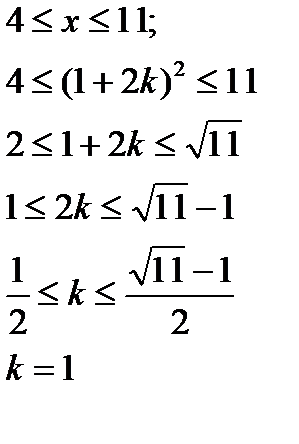

Ответ: x=9
11. Решите уравнение
 .
.
Решение:
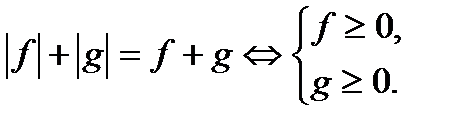



Ответ:  .
.
12. Решите неравенство 
 .
.
Решение:
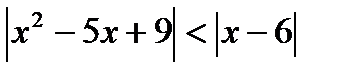
 (х
(х 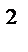 -5х+9)
-5х+9)  <(х-6)
<(х-6) 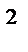
 (х
(х 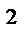 -5х+9)
-5х+9)  -(х-6)
-(х-6)  <0
<0 
 (х
(х  -6х+15)(х
-6х+15)(х  -4х+3)<0
-4х+3)<0  х
х  -4х+3<0
-4х+3<0  1<x<3.
1<x<3.
Ответ: (1;3).
12. Решить неравенство: 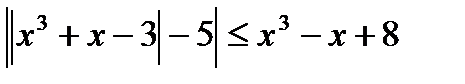 .
.
Решение:
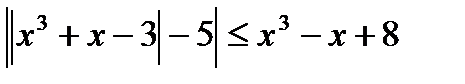






 .
.
Ответ: 
Дата добавления: 2015-10-21; просмотров: 68 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Необходимые сведения из теории | | | Способ раскрытия модуля. |