
|
Читайте также: |
Абсолютной величиной (модулем) числа х (обозначается | х |) называется само это число, если оно положительно или равно 0, и противоположное ему число, если это число отрицательно. В формальной записи:
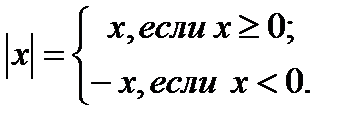
Геометрически | х | - это расстояние от точки х координатной прямой до начала координат.
Свойства модуля:
1) 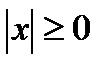 ; 2)
; 2) 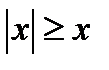 ; 3)
; 3) 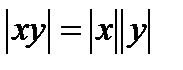 ;
;
4) 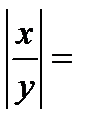
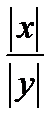 , если у
, если у 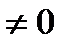 ; 5)
; 5)  ;
;
6) 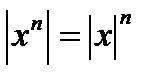 , n
, n 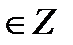 ;
;
7) а) 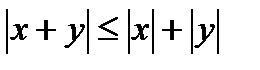 ; б)
; б) 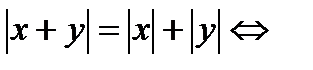 х и у одного знака;
х и у одного знака;
8) а)  ; б)
; б) 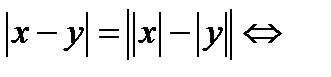 х и у одного знака.
х и у одного знака.
Стандартный алгоритм решения уравнений и неравенств с модулем.
Для решения уравнений и неравенств, содержащих модуль, имеется стандартный алгоритм, вытекающий из самого определения модуля: «освободиться» от символа модуля всегда можно, рассмотрев возможные знаки выражения, стоящего под этим символом или все необходимые комбинации знаков, когда символов модуля несколько. Главное при этом – не ошибиться при рассмотрении возможных комбинаций и не забыть проверить, удовлетворяют ли корни, полученные в каждом конкретном случае, условиям этого случая.
Нестандартные способы решения уравнений и неравенств с модулем.
1. Уравнения вида 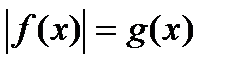 .
.
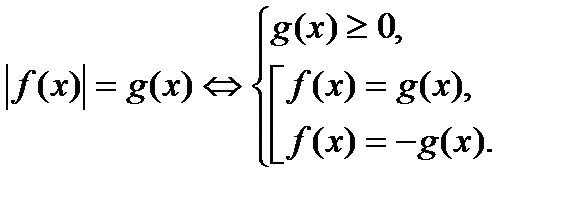
2. Уравнения вида  .
.


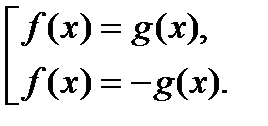
3. Уравнения вида 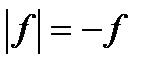
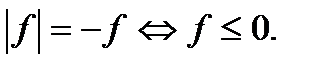
4. Уравнения вида 

5. Уравнения вида 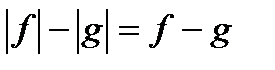
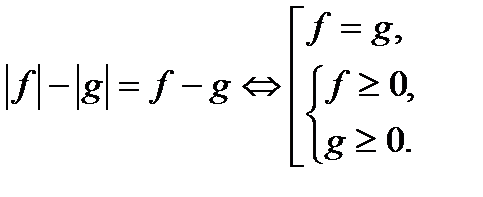
6. Уравнения вида 

7. Уравнения вида 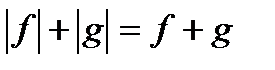
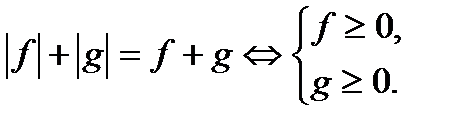
8. Уравнения вида 
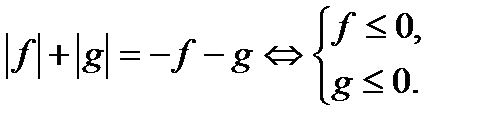
9. Неравенства вида 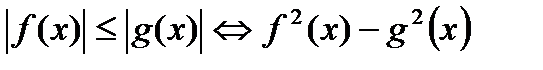 .
.
10. Неравенства вида 
11. Неравенства вида 
Дата добавления: 2015-10-21; просмотров: 83 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи для работы в аудитории | | | Примеры решения задач. |