Необходимые сведения из теории. Арифметическая прогрессия

Арифметическая прогрессия. Числовая последовательность 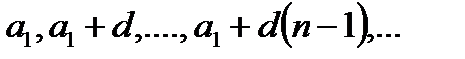, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом 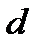,называется арифметической прогрессией. Число 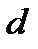называется разностью прогрессии, 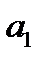- первый член прогрессии. Любой член арифметической прогрессии вычисляется по формуле:

;

.

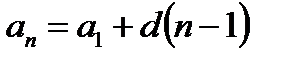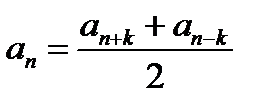Сумма 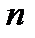первых членов арифметической прогрессии вычисляется по формуле:

.

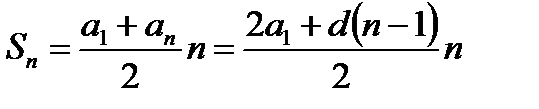Геометрическая прогрессия. Числовая последовательность 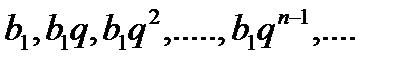, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число 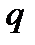, называется геометрической

прогрессией. Число 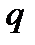называется знаменателем прогрессии. Любой член геометрической прогрессии вычисляется по формуле:

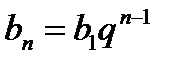
Сумма 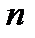первых членов геометрической прогрессии вычисляется по формуле:

Бесконечно убывающая геометрическая прогрессия. Это геометрическая прогрессия, у которой 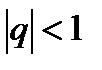. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии, а именно: это число, к которому неограниченно приближается сумма 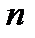первых членов рассматриваемой прогрессии при неограниченном возрастании числа 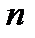. Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:

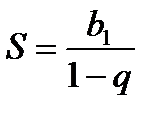
Дата добавления: 2015-10-21